【数据结构与算法】系列三十二 - 图（最短路径）

发表于 | 分类于
| 字数统计 3.7k 字 | 阅读时长 16 分钟

。。。

一、最短路径

最短路径是指两顶点之间权值之和最小的路径（有向图、无向图均适用，不能有负权环）。

1.1. 有权图

有向图：

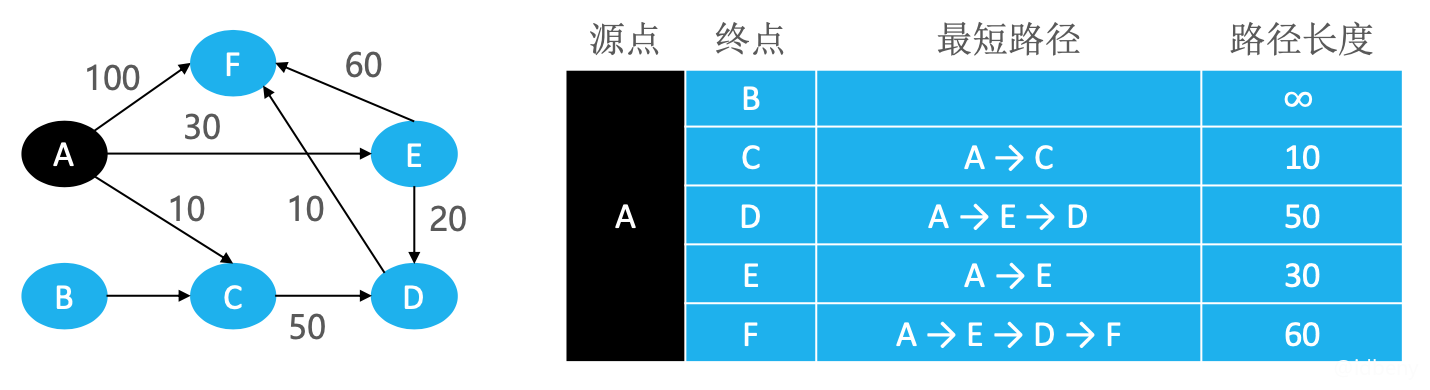
无向图：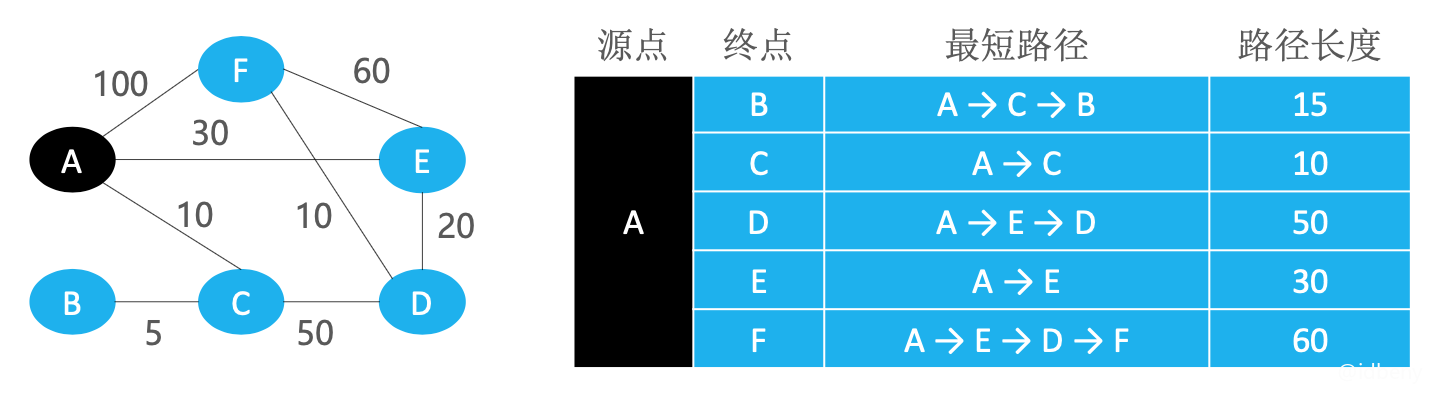

1.2. 无权图

无权图相当于是全部边权值为1的有权图。

有向图：

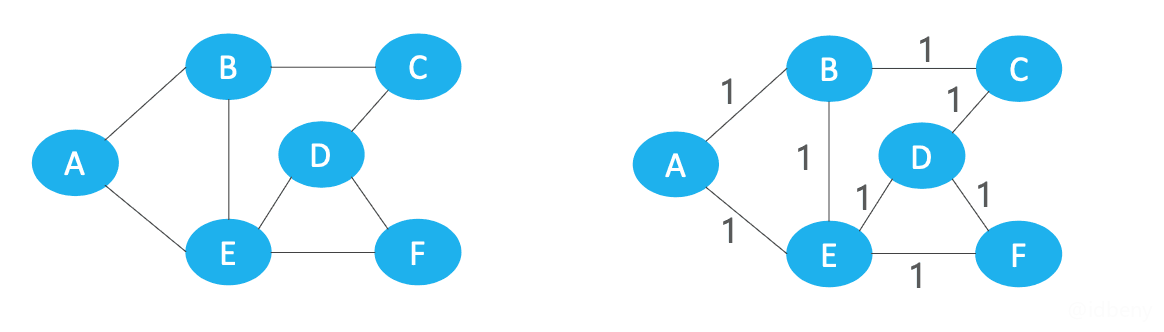
无向图：

1.3. 负权

1.3.1. 负权边

有负权边，但没有负权环时，存在最短路径。

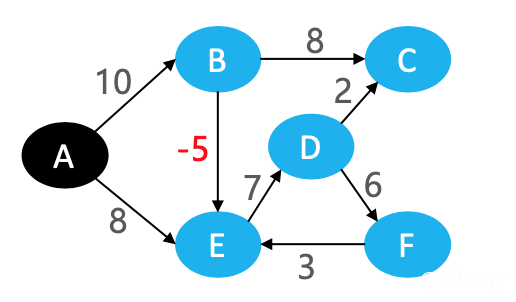
A到E的最短路径是：A → B → E。

1.3.2. 负权环

有负权环时，不存在最短路径。

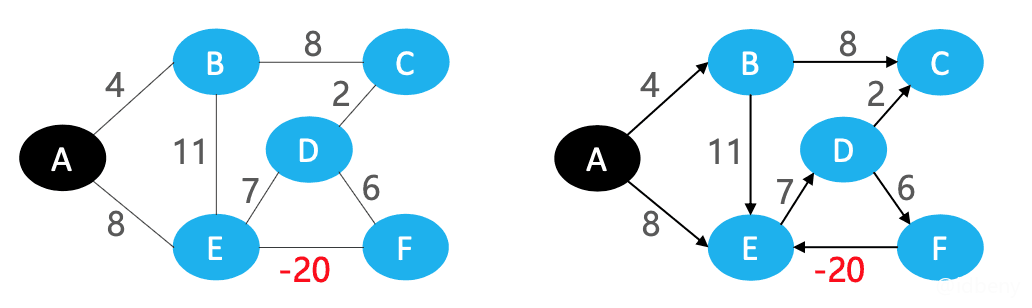
通过负权环时，A到E的路径可以无限短：A → E → D → F → E → D → F → E → D → F → E → D → F → E → ......。

最短路径的典型应用之一：路径规划问题。

求解最短路径的3个经典算法：

  • 单源最短路径算法
    • Dijkstra（迪杰斯特拉算法）
    • Bellman-Ford（贝尔曼-福特算法）
  • 多源最短路径算法
    • Floyd（弗洛伊德算法）

二、Dijkstra

Dijkstra属于单源最短路径算法（由荷兰的科学家Edsger Wybe Dijkstra发明，曾在1972年获得图灵奖），用于计算一个顶点到其他所有顶点的最短路径。

使用前提：不能有负权边。

时间复杂度：可优化至O(ElogV)，E是边数量，V是节点数量。

Dijkstra的原理其实跟生活中的一些自然现象完全一样。例如，把每1个顶点想象成是1块小石头，每1条边想象成是1条绳子，每一条绳子都连接着2块小石头，边的权值就是绳子的长度。将小石头和绳子平放在一张桌子上（下图是一张俯视图，图中黄颜色的是桌子）。

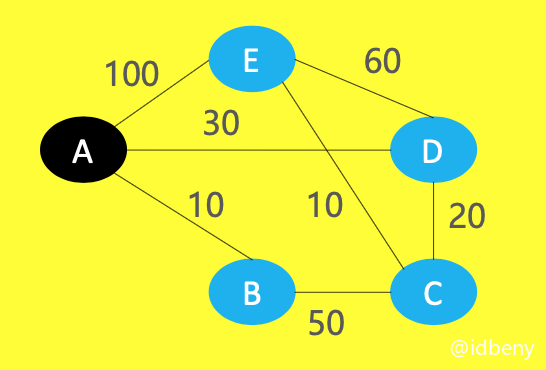
接下来想象一下，手拽着小石头A，慢慢地向上提起来，远离桌面，B、D、C、E会依次离开桌面，最后绷直的绳子就是A到其他小石头的最短路径。

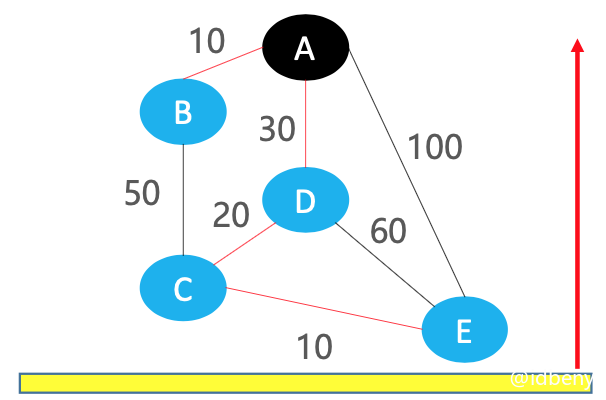
有一个很关键的信息：后离开桌面的小石头，都是被先离开桌面的小石头拉起来的（虽然是废话，但是代码执行中会不断用到该信息）。

2.1. 执行过程

如下图，就是求源头A到其他点的最短路径。

  1. A是源头（黑色），下一个被拉起的点必然是E、D、B（红色）其中一个，因为这些点直接连接A，所以更新A点到这几个终点的距离。

  1. A距离E、D、B最短的是AB（权值10）。此时A和B都已经被拉起，由于后离开桌面的小石头，都是被先离开桌面的小石头拉起来的，所以C和E、D一样都成为下次被拉起之一（更新A到终点C的路径和长度）。

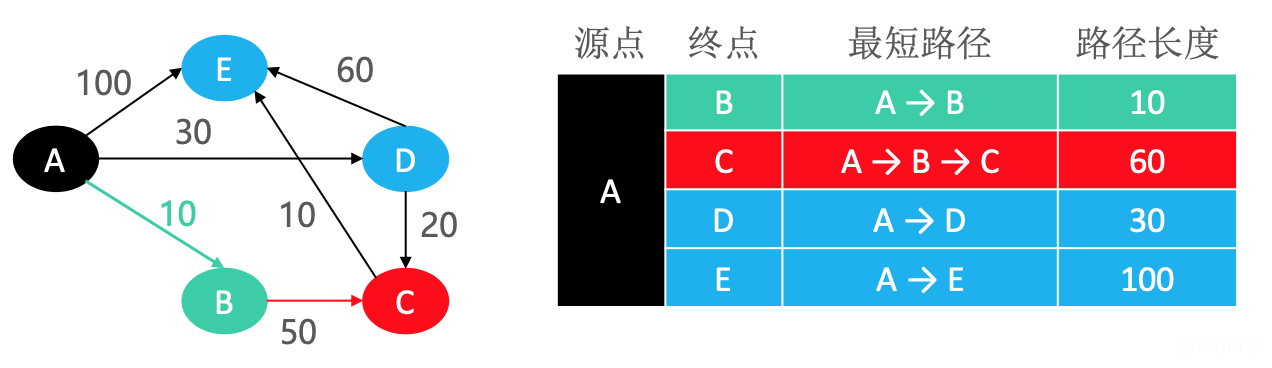
  • 注意：由于D还没离开，所以不可能可存在A → D → C。
  1. A距离C、D、E最短的是AD（权值30）。此时A、B、D都已经被拉起。由于D被拉起，所以出现了新的路径（ADE和ADC）。新的路径比之前路径更短（之前到达E的路径是AE，到达C的路径是ABC），因此更新到达终点E和C的路径和长度。

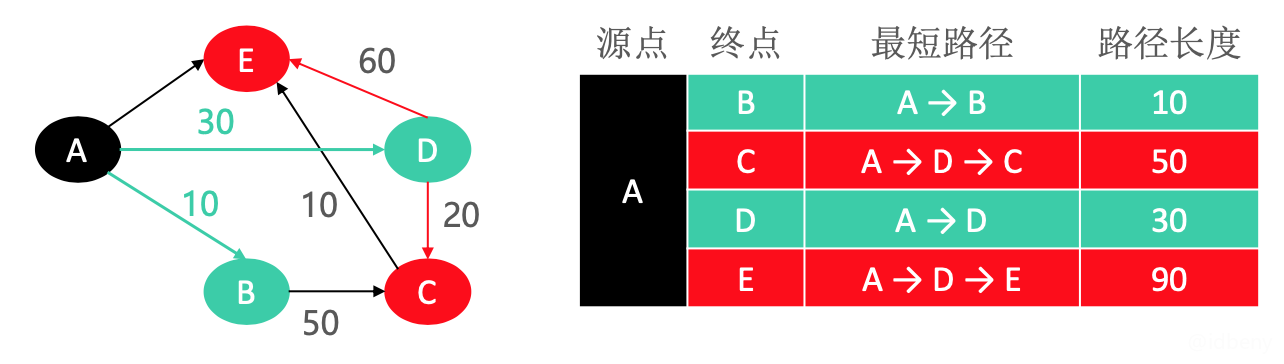
  1. A距离C、E最短的是ADC（权值50）。此时A、B、C、D都已经被拉起。由于C被拉起，所以出现了新的路径（ADCE）。新的路径比之前路径更短（之前到达E的路径是ADE），因此更新到达终点E的路径和长度。

  1. 最终E也被拉起。至此，A点到其他点的最短路径都已经确定。

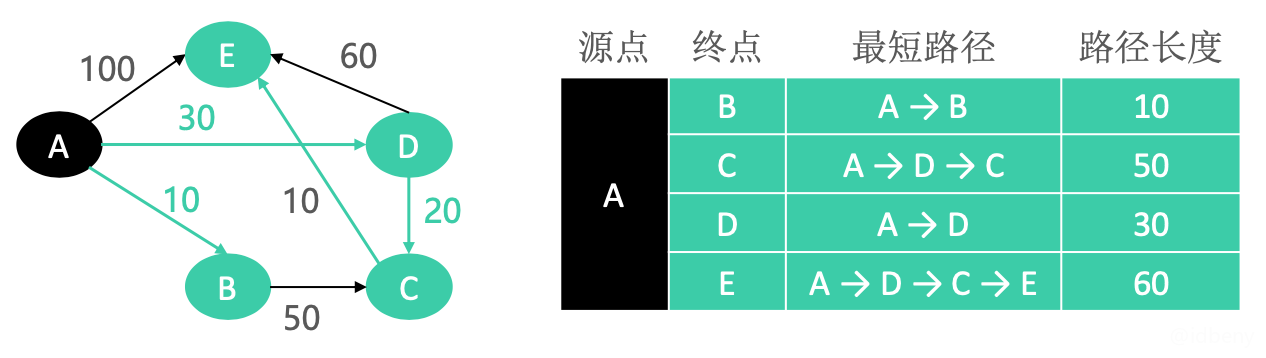
上面流程3、4都是发现了一条到达一个顶点的更短路径，如点A到达点E最短路径是100（AE），但当D被拉起后，发现可以通过D到达E，并且路径更短（到达E的最短路径是ADE），此时更新到达E的路径长度叫做松弛操作。

松弛操作（Relaxation）：更新2个顶点之间的最短路径。这里一般是指更新源点到另一个点的最短路径。

松弛操作的意义：尝试找出更短的最短路径。

对松弛两字的理解：假设两个顶点之间连接一条长度100的绳子，当两点靠拢时，绳子就会出现松弛现象，但是两点之间直线距离在变短（更新最短路径）。

2.2. 具体实现

下面的代码为了方便理解，在找最小路径时没有用到最小堆（用的是循环），所以代码时间复杂度并不是O(ElogV)，在实际开发中可以把对应方法换成最小堆。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
// 图的实现
public class ListGraph<V, E> extends Graph<V, E> {
  public ListGraph(WeightManager<E> weightManager) {
    super(weightManager);
  }

  // 比较器
  private Comparator<Edge<V, E>> edgeComparator = (Edge<V, E> e1, Edge<V, E> e2) -> {
    return weightManager.compare(e1.weight, e2.weight);
  };

  /**
   * 获取最短路径
   * @param begin 源头
   * @return begin到达其他顶点最短路径
   */ 
  public Map<V, PathInfo<V, E>> shortestPath(V begin) {
    return dijkstra(begin);
  }

  private Map<V, PathInfo<V, E>> dijkstra(V begin) {
    Vertex<V, E> beginVertex = vertices.get(begin);
    if (beginVertex == null) return null;

    Map<V, PathInfo<V, E>> selectedPaths = new HashMap<>();
    Map<Vertex<V, E>, PathInfo<V, E>> paths = new HashMap<>();
    // 第一种初始化做法
    for (Edge<V, E> edge : beginVertex.outEdges) {
      PathInfo<V, E> path = new PathInfo<>();
      path.weight = edge.weight;
      path.edges.add(edge);
      paths.put(edge.to, path);
    }
    // 第二种初始化做法：此处可参考Bellman-Ford的做法（让每条边都做松弛）
    // paths.put(beginVertex, new PathInfo<>(weightManager.zero()));

    while (!paths.isEmpty()) {
      Entry<Vertex<V, E>, PathInfo<V, E>> minEntry = getMinPath(paths);
      // minVertex离开桌面
      Vertex<V, E> minVertex = minEntry.getKey();
      PathInfo<V, E> minPath = minEntry.getValue();
      selectedPaths.put(minVertex.value, minPath);
      paths.remove(minVertex);
      // 对它的minVertex的outEdges进行松弛操作
      for (Edge<V, E> edge : minVertex.outEdges) {
        // 如果edge.to已经离开桌面，就没必要进行松弛操作
        if (selectedPaths.containsKey(edge.to.value)) continue;
        relaxForDijkstra(edge, minPath, paths);
      }
    }

    // 源头不需要做松弛操作（针对无向图）
    selectedPaths.remove(begin);
    return selectedPaths;
  }

  /**
   * 松弛
   * 
   * @param edge     需要进行松弛的边
   * @param fromPath edge的from的最短路径信息
   * @param paths    存放着其他点（对于dijkstra来说，就是还没有离开桌面的点）的最短路径信息
   */
  private void relaxForDijkstra(Edge<V, E> edge, PathInfo<V, E> fromPath, Map<Vertex<V, E>, PathInfo<V, E>> paths) {
    // 新的可选择的最短路径：beginVertex到edge.from的最短路径 + edge.weight
    // weightManager是对外部开放的接口，需要自定义实现，因为weight不一定是int
    E newWeight = weightManager.add(fromPath.weight, edge.weight);
    // 以前的最短路径：beginVertex到edge.to的最短路径
    PathInfo<V, E> oldPath = paths.get(edge.to);
    if (oldPath != null && weightManager.compare(newWeight, oldPath.weight) >= 0) return;

    if (oldPath == null) {
      oldPath = new PathInfo<>();
      paths.put(edge.to, oldPath);
    } else {
      oldPath.edges.clear();
    }

    oldPath.weight = newWeight;
    // 原来的路径信息
    oldPath.edges.addAll(fromPath.edges);
    // 把最新的边添加到路径中
    oldPath.edges.add(edge);
  }

  /**
   * 从paths中挑一个最小的路径出来
   * 
   * @param paths
   * @return
   */
  private Entry<Vertex<V, E>, PathInfo<V, E>> getMinPath(Map<Vertex<V, E>, PathInfo<V, E>> paths) {
    Iterator<Entry<Vertex<V, E>, PathInfo<V, E>>> it = paths.entrySet().iterator();
    Entry<Vertex<V, E>, PathInfo<V, E>> minEntry = it.next();
    while (it.hasNext()) {
      Entry<Vertex<V, E>, PathInfo<V, E>> entry = it.next();
      if (weightManager.compare(entry.getValue().weight, minEntry.getValue().weight) < 0) {
        minEntry = entry;
      }
    }
    return minEntry;
  }

  // other code...
}

// 抽象类（图的公共方法都在这里）
public abstract class Graph<V, E> {
  protected WeightManager<E> weightManager;
  
  public Graph(WeightManager<E> weightManager) {
    this.weightManager = weightManager;
  }

  // 自定义权值管理接口
  public interface WeightManager<E> {
    // 比较
    int compare(E w1, E w2);
    // 相加
    E add(E w1, E w2); 
    // 源头和自身的最短路径（防止松弛操作时weight是null）
    E zero();
  }

  // 路径信息
  public static class PathInfo<V, E> {
    protected E weight;
    protected List<Edge<V, E>> edges = new LinkedList<>();
    public PathInfo() {}
    public PathInfo(E weight) {
      this.weight = weight;
    }
    public E getWeight() {
      return weight;
    }
    public void setWeight(E weight) {
      this.weight = weight;
    }
    public List<Edge<V, E>> getEdges() {
      return edges;
    }
    public void setEdges(List<Edge<V, E>> edges) {
      this.edges = edges;
    }
    @Override
    public String toString() {
      return "PathInfo [weight=" + weight + ", edges=" + edges + "]";
    }
  }

  // other code...
}

// 使用
public class Main {
  static WeightManager<Double> weightManager = new WeightManager<Double>() {
    public int compare(Double w1, Double w2) {
      return w1.compareTo(w2);
    }

    public Double add(Double w1, Double w2) {
      return w1 + w2;
    }

    @Override
    public Double zero() {
      return 0.0;
    }
  }
  
  Graph<Object, Double> graph = new ListGraph<>(weightManager);
  Map<Object, PathInfo<Object, Double>> sp = graph.shortestPath("A");

  // other code...
}

三、Bellman-Ford

Bellman-Ford也属于单源最短路径算法，支持负权边，还能检测出是否有负权环。

算法原理：对所有的边进行V – 1次松弛操作（V是节点数量。松弛操作也可能只需要1次），得到所有可能的最短路径。

时间复杂度：O(EV)，E是边数量，V是节点数量。

下图的最好情况是恰好从左到右的顺序对边进行松弛操作（对所有边仅需进行1次松弛操作就能计算出A到达其他所有顶点的最短路径）：

最坏情况是恰好每次都从右到左的顺序对边进行松弛操作（对所有边需进行V – 1次松弛操作才能计算出A到达其他所有顶点的最短路径）：

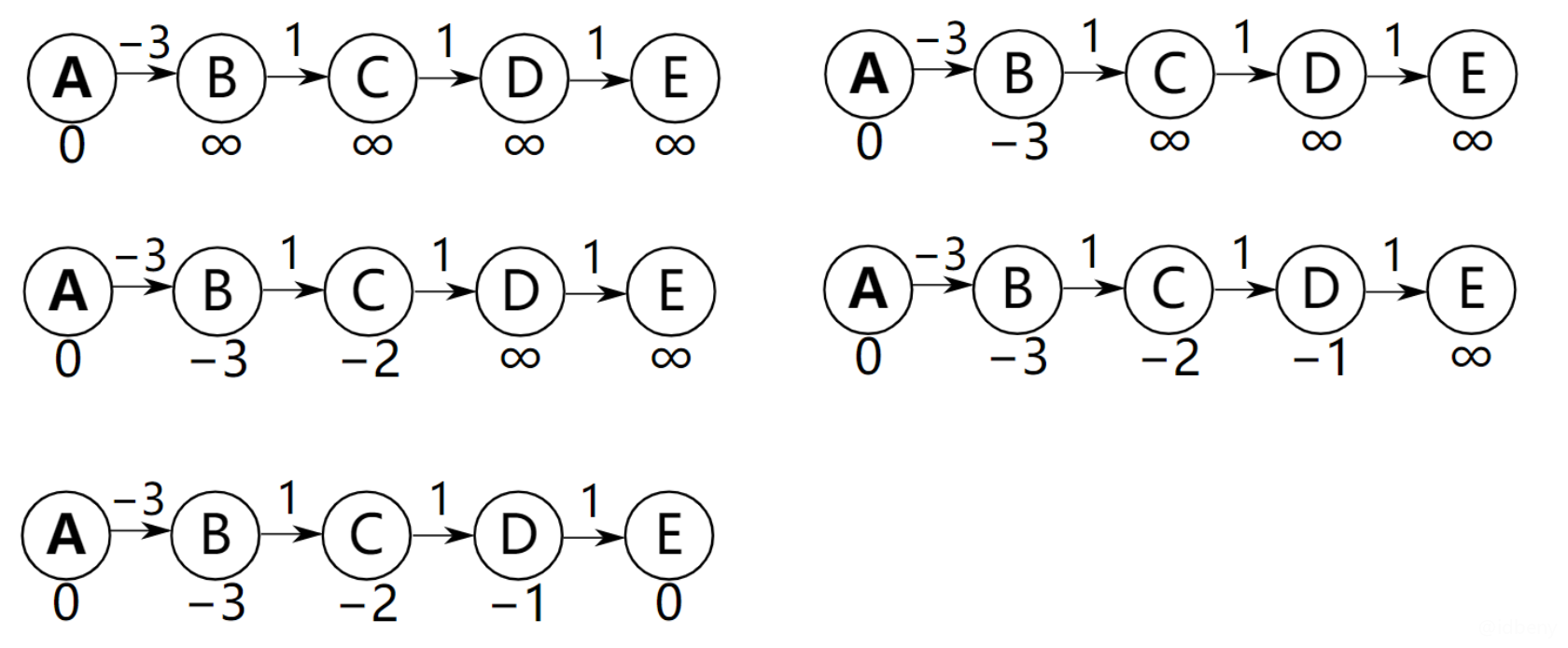
3.1. 执行过程

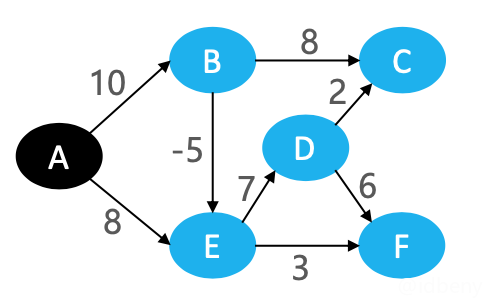
如上图，源头是A，一共8条边，假设每次松弛操作的顺序是：DC、DF、BC、ED、EF、BE、AE、AB（注意：图的边是用HashSet存储的，取出的顺序和添加的顺序是不一样的，但只要没有做添加和移除操作，每次取出的顺序都是一样的，也就导致有可能松弛顺序就是这样的）。

能否松弛成功就看起点的最短路径是否已经存在，如果不存在肯定松弛失败。

第1次松弛：由于源头是A，所以只有AE、AB松弛成功。

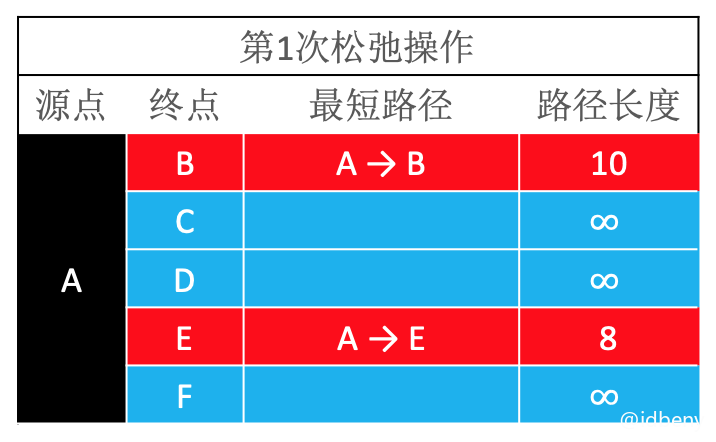
第2次松弛：BE优先AE做松弛操作，ABE路径长度是5，AE路径长度是8，所以AE松弛操作失败。AB无变化（蓝色表示）。

第3次松弛：更新最短路径和长度。

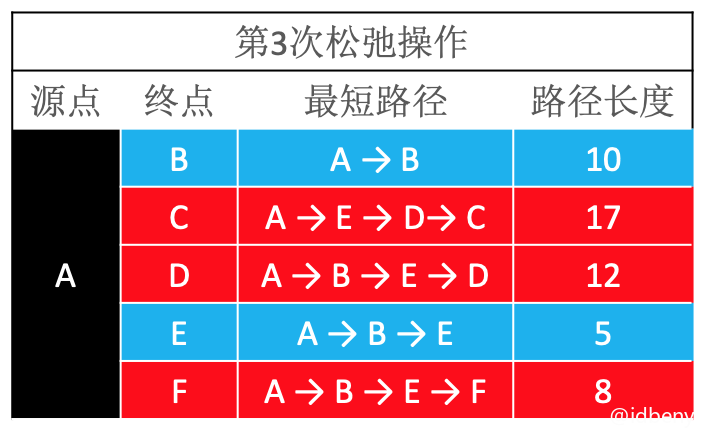
第4次松弛：

不难分析出，经过4次松弛操作之后，已经计算出了A到其他所有顶点的最短路径（及时后面还有更多次，结果也是一样的）。

3.2. 具体实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
private Map<V, PathInfo<V, E>> bellmanFord(V begin) {
  Vertex<V, E> beginVertex = vertices.get(begin);
  if (beginVertex == null) return null;

  Map<V, PathInfo<V, E>> selectedPaths = new HashMap<>();
  selectedPaths.put(begin, new PathInfo<>(weightManager.zero()));

  int count = vertices.size() - 1;
  for (int i = 0; i < count; i++) { // v - 1 次
    for (Edge<V, E> edge : edges) {
      // 获取起点的最短路径信息
      PathInfo<V, E> fromPath = selectedPaths.get(edge.from.value);
      // begin到from的最短路径可能是空的
      if (fromPath == null) continue;
      relax(edge, fromPath, selectedPaths);
    }
  }

  // 判断是否有负权环
  // V-1次操作后，还能进行松弛操作说明是有负权环的（每次都能找到最短路径）
  for (Edge<V, E> edge : edges) {
    PathInfo<V, E> fromPath = selectedPaths.get(edge.from.value);
    if (fromPath == null) continue;
    // 
    if (relax(edge, fromPath, selectedPaths)) {
      System.out.println("有负权环");
      return null;
    }
  }

  selectedPaths.remove(begin);
  return selectedPaths;
}

/**
 * 松弛（和dijkstra松弛代码不一样的是paths存放的key不同）
 * 
 * @param edge     需要进行松弛的边
 * @param fromPath edge的from的最短路径信息
 * @param paths    存放着其他点
 */
private boolean relax(Edge<V, E> edge, PathInfo<V, E> fromPath, Map<V, PathInfo<V, E>> paths) {
  // 新的可选择的最短路径：beginVertex到edge.from的最短路径 + edge.weight
  E newWeight = weightManager.add(fromPath.weight, edge.weight);
  // 以前的最短路径：beginVertex到edge.to的最短路径
  PathInfo<V, E> oldPath = paths.get(edge.to.value);
  if (oldPath != null && weightManager.compare(newWeight, oldPath.weight) >= 0) return false;

  if (oldPath == null) {
    oldPath = new PathInfo<>();
    paths.put(edge.to.value, oldPath);
  } else {
    oldPath.edges.clear();
  }

  oldPath.weight = newWeight;
  oldPath.edges.addAll(fromPath.edges);
  oldPath.edges.add(edge);

  return true;
}

四、Floyd

Floyd属于多源最短路径算法，能够求出任意2个顶点之间的最短路径，支持负权边。

时间复杂度：O(V^3)，效率比执行V次Dijkstra算法要好（每个顶点都作为源点执行一遍Dijkstra算法。V是顶点数量）。

4.1. 算法原理

从任意顶点i到任意顶点j的最短路径不外乎两种可能：

  1. 直接从i到j；
  2. 从i经过若干个顶点到j。

假设dist(i，j)为顶点i到顶点j的最短路径的距离，对于每一个顶点k，检查dist(i，k) + dist(k，j) < dist(i，j)是否成立。

  • 如果成立，证明从i到k再到j的路径比i直接到j的路径短，设置 dist(i，j) = dist(i，k) + dist(k，j)
  • 当我们遍历完所有节点k，dist(i，j)中记录的便是i到j的最短路径的距离（每个节点都会成为i、j、k）

伪代码：

1
2
3
4
5
6
7
8
9
for (int k = 0; k < V; k++) {
  for (int k = 0; i < V; i++) {
    for (int k = 0; j < V; j++) {
      if (dist(i, k) + dist(k, j) < dist(i, j)) {
        dist(i, j) = dist(i, k) + dist(k, j);
      }
    }
  }
}

4.2. 具体实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
// 返回的是任意两个顶点之间的路径信息
public Map<V, Map<V, PathInfo<V, E>>> shortestPath() {
  Map<V, Map<V, PathInfo<V, E>>> paths = new HashMap<>();
  // 初始化
  for (Edge<V, E> edge : edges) {
    Map<V, PathInfo<V, E>> map = paths.get(edge.from.value);
    if (map == null) {
      map = new HashMap<>();
      paths.put(edge.from.value, map);
    }

    PathInfo<V, E> pathInfo = new PathInfo<>(edge.weight);
    pathInfo.edges.add(edge);
    map.put(edge.to.value, pathInfo);
  }

  vertices.forEach((V v2, Vertex<V, E> vertex2) -> {
    vertices.forEach((V v1, Vertex<V, E> vertex1) -> {
      vertices.forEach((V v3, Vertex<V, E> vertex3) -> {
        // 同一个点不需要做任何操作
        if (v1.equals(v2) || v2.equals(v3) || v1.equals(v3)) return;

        // v1 -> v2
        PathInfo<V, E> path12 = getPathInfo(v1, v2, paths);
        if (path12 == null) return;

        // v2 -> v3
        PathInfo<V, E> path23 = getPathInfo(v2, v3, paths);
        if (path23 == null) return;

        // v1 -> v3
        PathInfo<V, E> path13 = getPathInfo(v1, v3, paths);

        E newWeight = weightManager.add(path12.weight, path23.weight);
        if (path13 != null && weightManager.compare(newWeight, path13.weight) >= 0) return;

        if (path13 == null) {
          path13 = new PathInfo<V, E>();
          paths.get(v1).put(v3, path13);
        } else {
          path13.edges.clear();
        }

        path13.weight = newWeight;
        path13.edges.addAll(path12.edges);
        path13.edges.addAll(path23.edges);
      });
    });
  });

  return paths;
}

private PathInfo<V, E> getPathInfo(V from, V to, Map<V, Map<V, PathInfo<V, E>>> paths) {
  Map<V, PathInfo<V, E>> map = paths.get(from);
  return map == null ? null : map.get(to);
}