。。。
一、递归
递归(Recursion):函数(方法)直接或间接调用自身。是一种常用的编程技巧。
1 | // 直接调用 |
1.1. 函数的调用过程
1 | public static void main(String[] args) { |
程序运行main函数时,会为它在栈区分配一段连续的内存空间,运行到test1时,同样也是在栈区为其分配一段内存,当test1执行结束后,系统会自动回收其在栈区的内存。运行到test2时,同样在栈区为其分配一段内存,执行test2函数内部代码时,调用test3函数,只有test3函数执行完毕且内存被回收后才能释放test2函数的内存。

1.2. 函数的递归调用过程
1 | public static void main(String[] args) { |
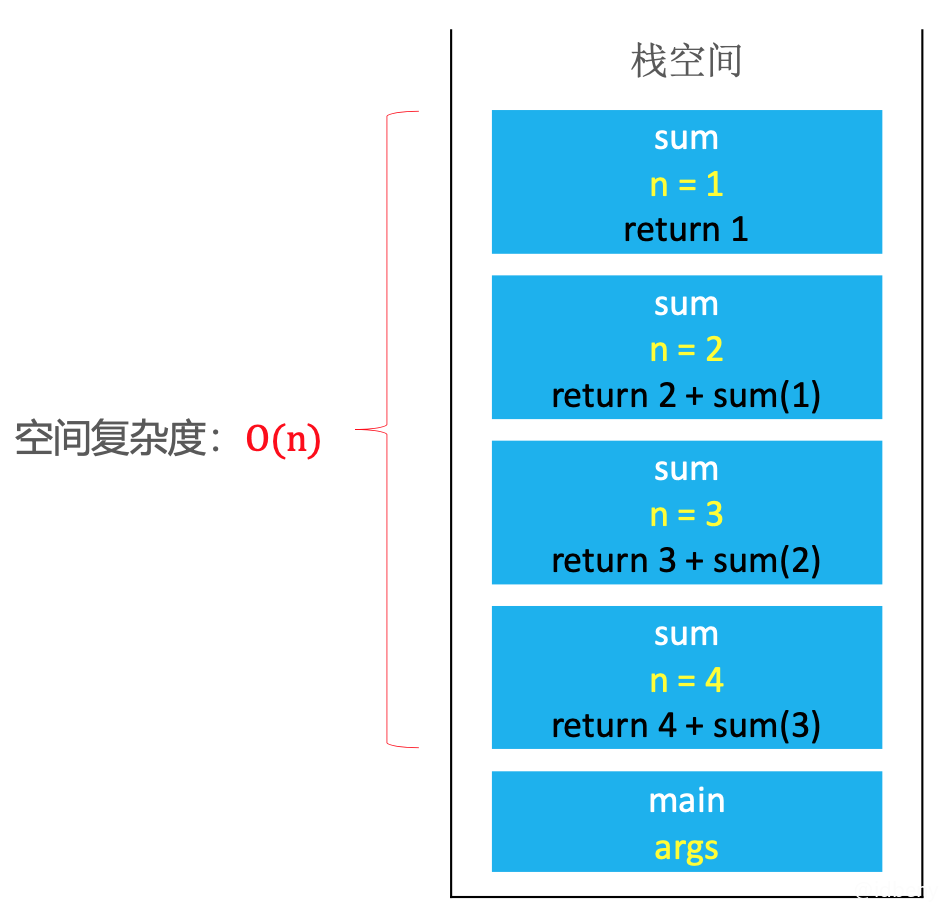
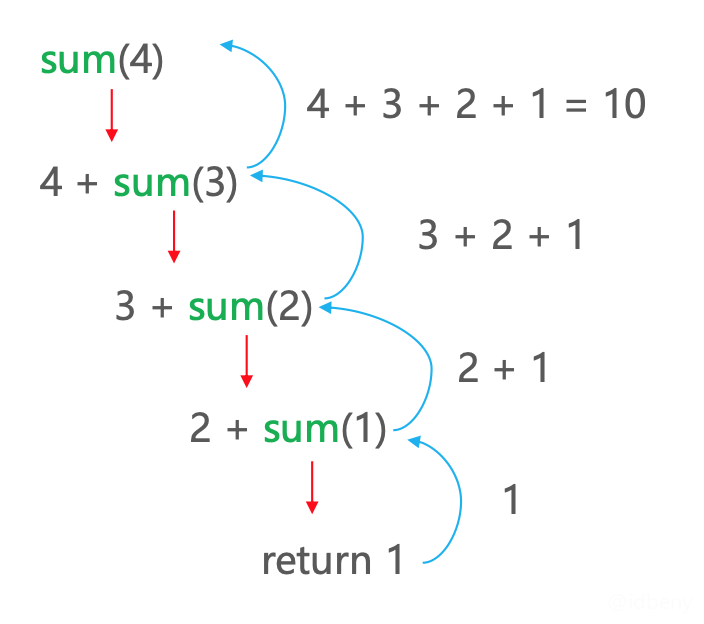
如果递归调用没有终止,将会一直消耗栈空间,最终导致栈内存溢出(Stack Overflow)。所以必需要有一个明确的结束递归的条件,也叫作边界条件、递归基。
1.3. 示例分析
求1+2+3+...+(n-1)+n, (n>0)的和。
1.3.1. 递归
1 | int sum(int n) { |
总消耗时间T(n) = T(n−1) + O(1),因此:
时间复杂度:O(n)
空间复杂度:O(n)
1.3.2. for循环
1 | int sum(int n) { |
时间复杂度:O(n)
空间复杂度:O(1)
1.3.3. 等差数列求和
1 | int sum(int n) { |
时间复杂度:O(1)
空间复杂度:O(1)
注意:递归求出来的很有可能不是最优解(时间和空间复杂度),也有可能是最优解。但使用递归不是为了求得最优解,是为了简化解决问题的思路,代码会更加简洁。
1.4. 基本思想
拆解问题:
- 把规模大的问题变成规模较小的同类型问题
- 规模较小的问题又不断变成规模更小的问题
- 规模小到一定程度可以直接得出它的解
求解:
- 由最小规模问题的解得出较大规模问题的解
- 由较大规模问题的解不断得出规模更大问题的解
- 最后得出原来问题的解
凡是可以利用上述思想解决问题的,都可以尝试使用递归。很多链表、二叉树相关的问题都可以使用递归来解决(因为链表、二叉树本身就是递归的结构(大链表中包含小链表,大二叉树中包含小二叉树))。
1.5. 使用技巧
- 明确函数的功能
- 先不要去思考里面代码怎么写,首先搞清楚这个函数的干嘛用的,能完成什么功能?
- 明确原问题与子问题的关系
- 寻找
f(n)与f(n – 1)的关系
- 寻找
- 明确递归基(边界条件)
- 递归的过程中,子问题的规模在不断减小,当小到一定程度时可以直接得出它的解
- 寻找递归基,相当于是思考:问题规模小到什么程度可以直接得出解。
二、经典案例
2.1. 斐波那契数列
斐波那契数列:1、1、2、3、5、8、13、21、34、......
1 | F(1) = 1,F(2) = 1, F(n) = F(n-1) + F(n-2) (n≥3) |
编写一个函数求第n项斐波那契数:
1 | int fib(int n) { |
根据递推式T(n) = T(n−1) + T(n−2) + O(1),可得知时间复杂度是O(2^n),空间复杂度是O(n)。
递归调用的空间复杂度 = 递归深度 * 每次调用所需的辅助空间
如下图,出现了大量重复计算的步骤,而且每次调用fib只做加法操作,所以空间复杂度是O(n)。每次fib都被分裂为两个更小的fib执行,所以每次fib都是乘以2的执行次数,因此时间复杂度是O(2^n)。
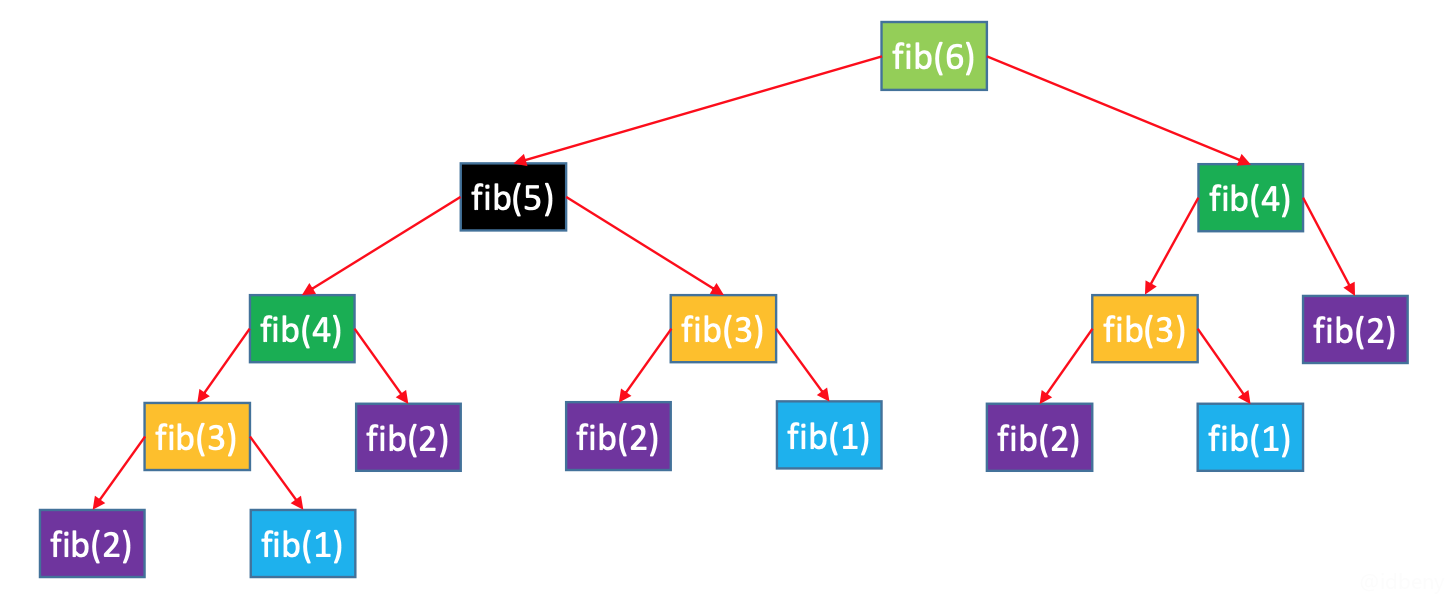
每次执行fib(n - 1),只要还未结束调用,就不会执行fib(n - 2)。但fib(n - 1)包含fib(n - 2)所有执行流程(这是一种“自顶向下”的调用过程)。因此我们可以把计算过的结果存下来,避免大量的重复计算。
2.1.1. 优化1 - 记忆化
用数组存放计算过的结果,避免重复计算。
1 | int fib(int n) { |
时间复杂度:O(n)
空间复杂度:O(n)
2.1.2. 优化2 - 去除递归
下面代码是一种“自底向上”的计算过程。
1 | int fib(int n) { |
时间复杂度:O(n)
空间复杂度:O(n)
2.1.3. 优化3 - 滚动数组
由于每次运算只需要用到数组中的2个元素,所以可以使用滚动数组来优化。
滚动数组:固定数组元素数量,反复循环更新元素值。
1 | int fib(int n) { |
时间复杂度:O(n)
空间复杂度:O(1)
乘、除、模运算效率较低,建议用位运算取代。
1 | int fib(int n) { |
2.1.4. 优化4 - 累加
1 | int fib(int n) { |
时间复杂度:O(n)
空间复杂度:O(1)
2.1.5. 优化5 - 特征方程
斐波那契数列有个线性代数解法:特征方程。

1 | int fib(int n) { |
时间复杂度、空间复杂度取决于pow函数(至少可以低至O(logn))。
2.2. 上楼梯(跳台阶)
楼梯有n阶台阶,上楼可以一步上1阶,也可以一步上2阶,走完n阶台阶共有多少种不同的走法?
假设n阶台阶有f(n)种走法,第1步有2种走法:
- 如果上1阶,那就还剩
n – 1阶,共f(n – 1)种走法 - 如果上2阶,那就还剩
n – 2阶,共f(n – 2)种走法
两种走法加起来就是总的走法,即f(n) = f(n – 1) + f(n – 2),跟斐波那契数列几乎一样,因此优化思路也是一致的。
1 | // 优化前 |
2.3. 汉诺塔(Hanoi)
编程实现把A的n个盘子移动到C(盘子编号是[1, n])。
要求:每次只能移动1个盘子,大盘子只能放在小盘子下面。

1个盘子:

2个盘子:
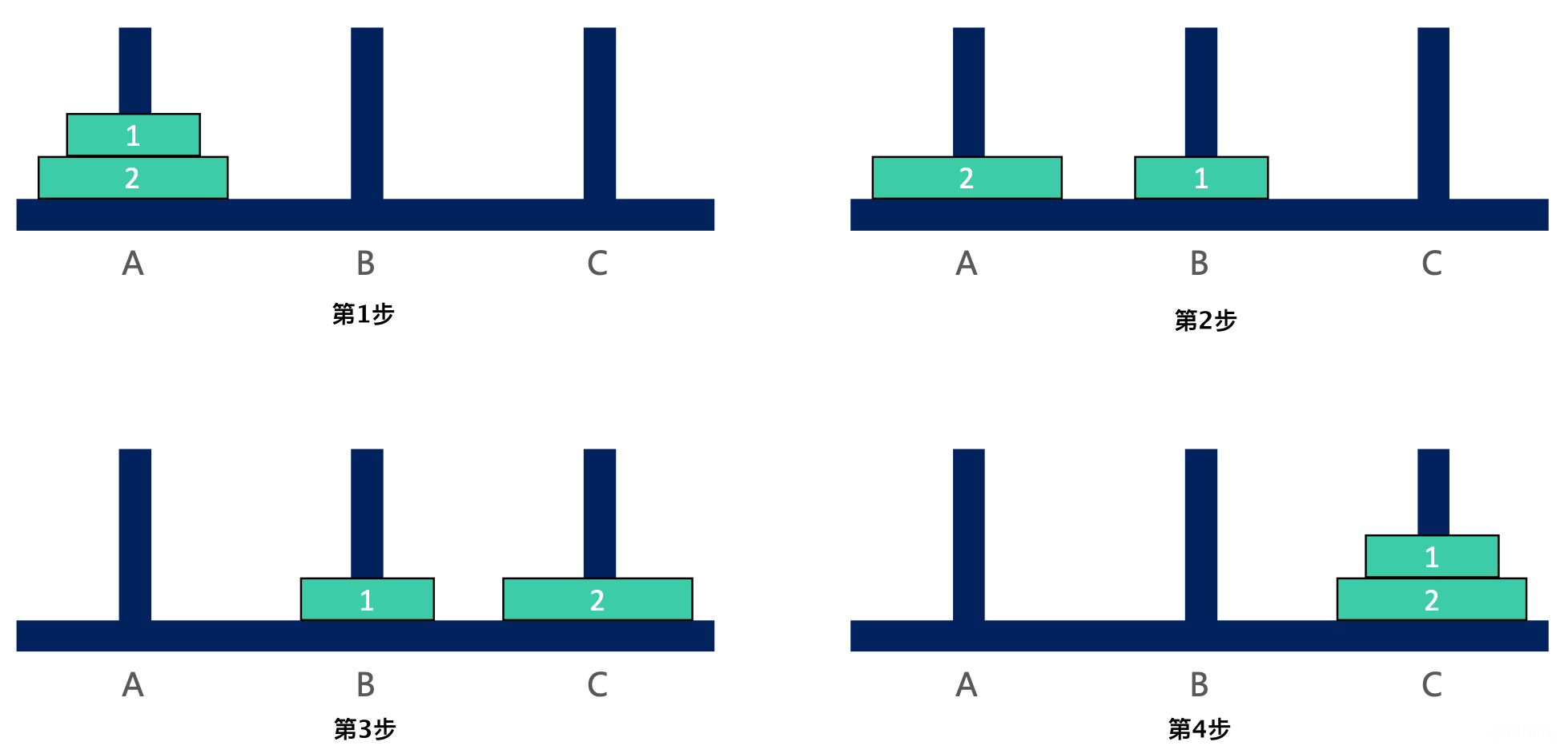
3个盘子:
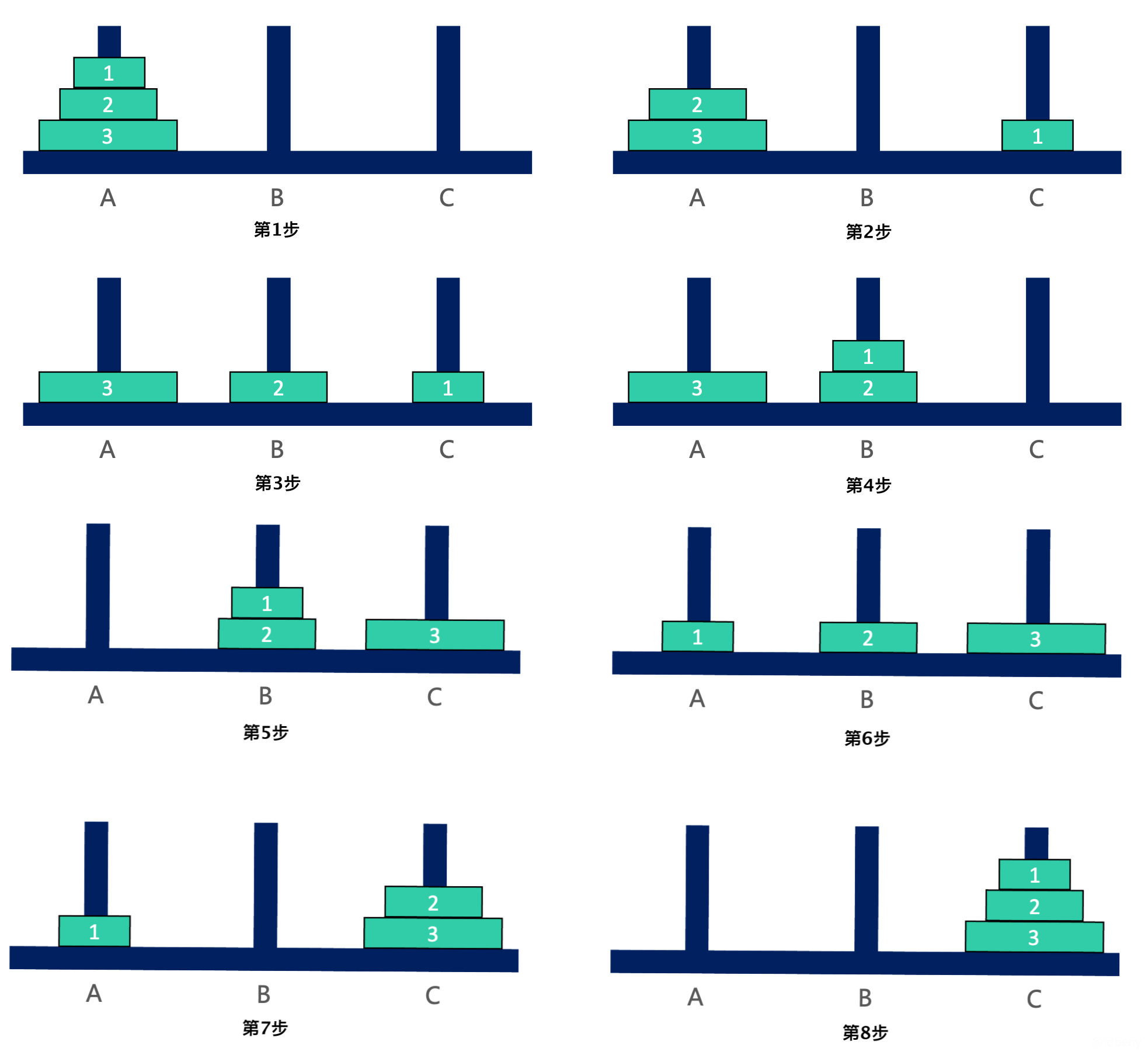
2.3.1. 思路
其实分2种情况讨论即可:
- 当
n == 1时,直接将盘子从A移动到C - 当
n > 1时,可以拆分成3大步骤- 将
n – 1个盘子从A移动到B; - 将编号为
n的盘子从A移动到C; - 将
n – 1个盘子从B移动到C。
- 步骤1和3明显是个递归调用。
- 将
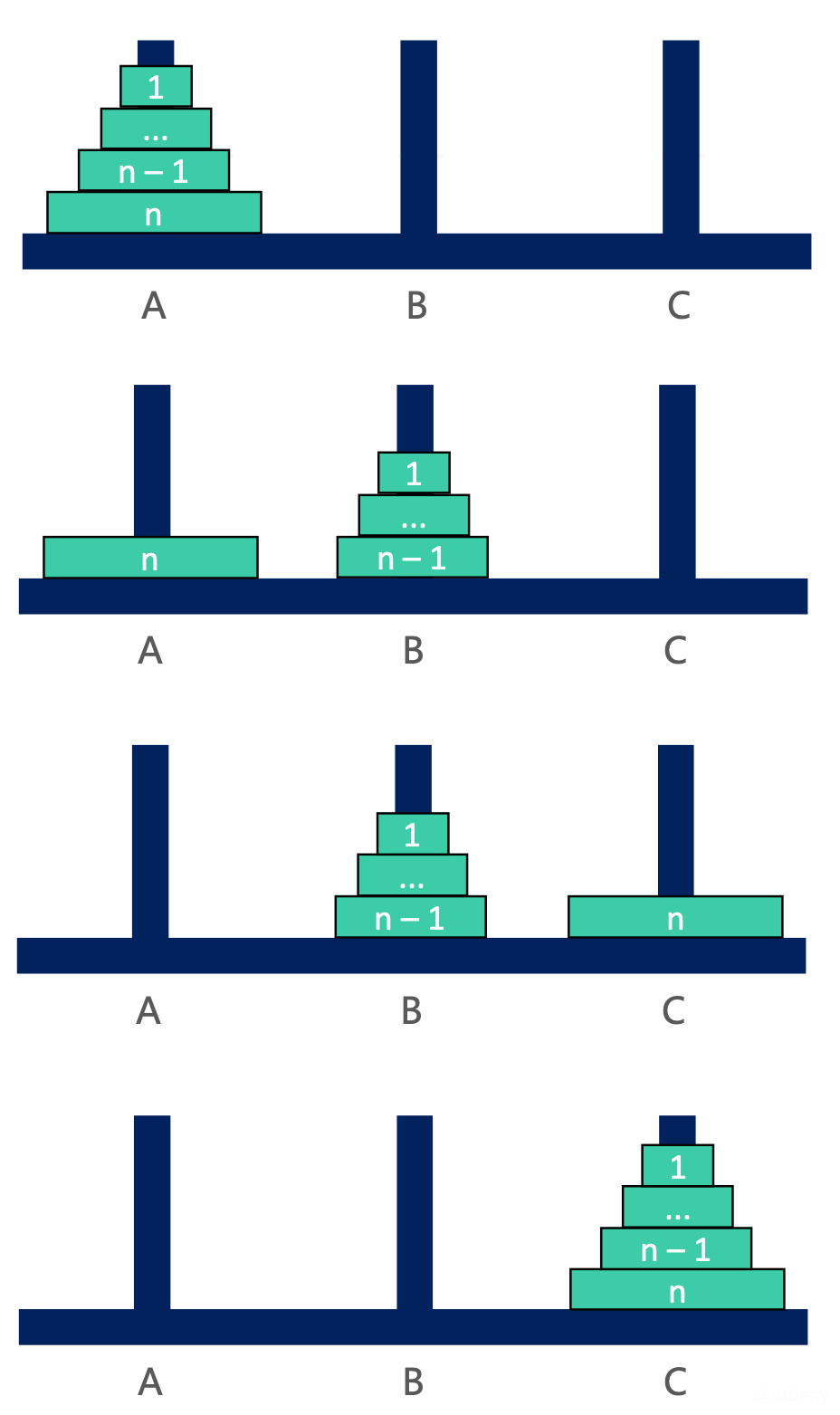
2.3.2. 实现
1 | /** |
T(n) = 2 * T(n−1) + O(1),因此时间复杂度是O(2^n),空间复杂度是O(n)。
三、递归转非递归
递归调用的过程中,会将每一次调用的参数、局部变量都保存在对应的栈帧(Stack Frame)中。
1 | public static void main(String[] args) { |
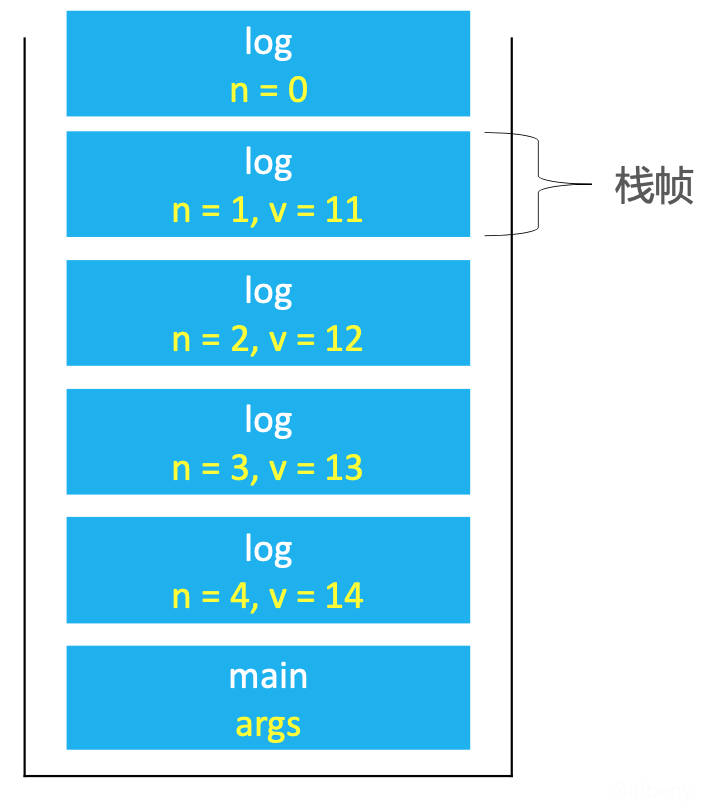
若递归调用深度较大,会占用比较多的栈空间,甚至会导致栈溢出。在有些时候,递归会存在大量的重复计算,性能非常差。这时可以考虑将递归转为非递归(递归100%可以转换成非递归)。
递归转非递归的万能方法:自己维护一个栈,来保存参数、局部变量(这个操作仅仅是把系统化转为自定义,空间复杂度依然没有得到优化)。
1 | // 栈帧 |
在某些时候,也可以重复使用一组相同的变量来保存每个栈帧的内容。如下面代码,重复使用变量i(想象成自定义对象)保存原来栈帧中的参数,空间复杂度从O(n)降到了O(1)。
1 | static void log(int n) { |
四、尾调用
尾调用(Tail Call):一个函数的最后一个动作是调用函数。
如果最后一个动作是调用自身,称为尾递归(Tail Recursion),是尾调用的特殊情况。
1 | void test1() { |
一些编译器能对尾调用进行优化,以达到节省栈空间的目的。如下图,每次都会重复利用test2的内存。
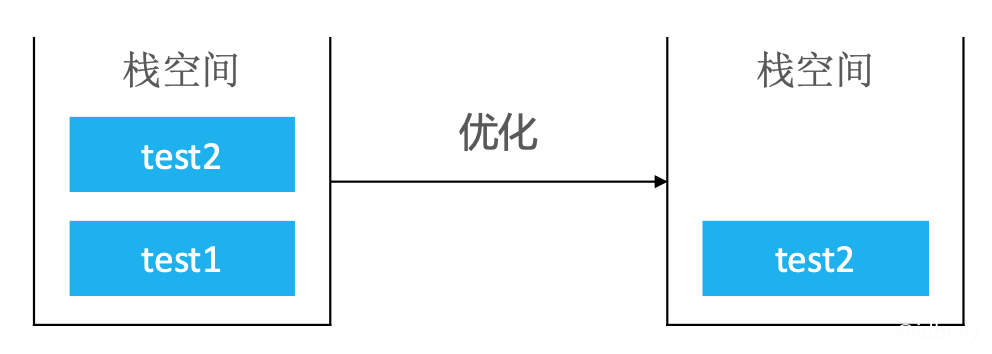
下面代码不是尾调用,因为它最后1个动作是乘法(n * 1)。
1 | // 阶乘 |
4.1. 尾调用优化
尾调用优化也叫做尾调用消除(Tail Call Elimination)。
如果当前栈帧上的局部变量等内容都不需要用了,当前栈帧经过适当的改变后可以直接当作被尾调用的函数的栈帧使用,然后程序可以jump到被尾调用的函数代码。
生成栈帧改变代码与jump的过程称作尾调用消除或尾调用优化。
尾调用优化让位于尾位置的函数调用跟goto语句性能一样高。
消除尾递归里的尾调用比消除一般的尾调用容易很多。比如Java虚拟机(JVM)会消除尾递归里的尾调用,但不会消除一般的尾调用(因为改变不了栈帧),因此尾递归优化相对比较普遍,平时的递归代码可以考虑尽量使用尾递归的形式。
4.2. 尾递归示例
4.2.1. 阶乘
求n的阶乘1*2*3*...*(n-1)*n (n>0)。
1 | int factorial(int n) { |
4.2.2. 斐波那契数列
1 | // 尾调用 |
