【数据结构与算法】系列三十一 - 图（拓扑排序/最小生成树）

一、AOV网

一项大的工程常被分为多个小的子工程，子工程之间可能存在一定的先后顺序，即某些子工程必须在其他的一些子工程完成后才能开始。

在现代化管理中，人们常用有向图来描述和分析一项工程的计划和实施过程，子工程被称为活动（Activity）。以顶点表示活动，有向边表示活动之间的先后关系，这样的图简称为AOV网（Activity On Vertex Network）。

有兴趣的同学可以去查阅资料了解一下什么是AOE网络。

标准的AOV网必须是一个有向无环图（Directed Acyclic Graph，简称 DAG)。

B依赖于A
C依赖于B
D依赖于B
E依赖于B、C、D
F依赖于E

提示：如果AOV网是一个有向有环图就会形成死循环，所以必须是一个有向无环图。

1.1. 拓扑排序

前驱活动：有向边起点的活动称为终点的前驱活动。只有当一个活动的前驱全部都完成后，这个活动才能进行。

后继活动：有向边终点的活动称为起点的后继活动。

什么是拓扑排序（Topological Sort）？将AOV网中所有活动排成一个序列，使得每个活动的前驱活动都排在该活动的前面。比如上图的拓扑排序结果是:A、B、C、D、E、F 或者 A、B、D、C、E、F（结果并不一定是唯一的）。

1.1.1. 思路

可以使用卡恩算法（Kahn于1962年提出）完成拓扑排序。

假设L是存放拓扑排序结果的列表。
1. 把所有入度为0的顶点放入L中，然后把这些顶点从图中去掉；
2. 重复操作1，直到找不到入度为0的顶点。
如果此时L中的元素个数和顶点总数相同，说明拓扑排序完成。
如果此时L中的元素个数少于顶点总数，说明原图中存在环，无法进行拓扑排序。

1.1.2. 实现

由于在实际排序代码中不能把顶点从图中删除（如果删除就会影响原来的数据），所以我们可以把每个顶点的入度信息记录下来，当入度为0时，就认为顶点被移除掉。

把入度为0的顶点放入到队列中（遍历入口）；
然后开始依次从队列中出队并放入到排序结果列表中，同时遍历出队顶点的出边，把边的终点入度从入度信息表中减1，当发现入度为0时，把该顶点放入到队列中，重复2，直到队列为空。

public List<V> topologicalSort() {
  // 排序结果
  List<V> list = new ArrayList<>();
  // 队列（存放度为0的顶点）
  Queue<Vertex<V, E>> queue = new LinkedList<>();
  // 顶点的入度信息
  Map<Vertex<V, E>, Integer> ins = new HashMap<>();
  // 初始化（将度为0的节点都放入队列）
  vertices.forEach((V v, Vertex<V, E> vertex) -> {
    int in = vertex.inEdges.size();
    if (in == 0) { // 入度为0的没有必要维护（记录）入度信息
      queue.offer(vertex);
    } else {
      ins.put(vertex, in);
    }
  });

  while (!queue.isEmpty()) {
    Vertex<V, E> vertex = queue.poll();
    // 放入排序结果中
    list.add(vertex.value);

    // 遍历出队顶点的出边（找出边的终点）
    for (Edge<V, E> edge : vertex.outEdges) {
      // 边的终点入度减1
      int toIn = ins.get(edge.to) - 1;
      if (toIn == 0) {
        queue.offer(edge.to);
      } else {
        ins.put(edge.to, toIn);
      }
    }
  }

  return list;
}

1.2. LeetCode

课程表：https://leetcode-cn.com/problems/course-schedule-ii/

二、生成树

生成树（Spanning Tree），也称为支撑树。连通图的极小连通子图（用最少边的连通图）就是生成树，它含有图中全部的n个顶点，恰好只有n – 1条边。

如下，第一个图是连通图，其它都是生成树：

2.1. 最小生成树

最小生成树（Minimum Spanning Tree，简称 MST），也称为最小权重生成树（Minimum Weight Spanning Tree）、最小支撑树。是所有生成树中，总权值最小的那棵，适用于有权的连通图（无向）。

如下，左图是有权连通图，右图是最小生成树：

最小生成树在许多领域都有重要的作用。例如，要在n个城市之间铺设光缆，使它们都可以通信，铺设光缆的费用很高，且各个城市之间因为距离不同等因素，铺设光缆的费用也不同，如何使铺设光缆的总费用最低（如上图，顶点代表城市，边代表光缆，权值代表长度）？

如果图的每一条边的权值都互不相同，那么最小生成树将只有一个，否则可能会有多个最小生成树。

求最小生成树的2个经典算法：

Prim（普里姆算法）
Kruskal（克鲁斯克尔算法）

在了解这两个算法之前，我们先看一下什么是切分？

2.2. 切分定理

切分（Cut）：把图中的节点分为两部分，称为一个切分。

下图有个切分C = (S, T)，S = {A, B, D}，T = {C, E}：

横切边（Crossing Edge）：如果一个边的两个顶点，分别属于切分的两部分，这个边称为横切边。比如上图的边BC、BE、DE就是横切边。

切分定理：给定任意切分，横切边中权值最小的边必然属于最小生成树（如上图，切分为两部分，而要形成连通图必须至少有一条横切边连接两部分，横切边权值越小，形成的连通图总权值也就越小，也就形成了最小生成树）。

2.3. Prim算法

假设G = (V，E)（V是顶点，E是边）是有权的连通图（无向），A是G中最小生成树的边集（也就是组成最小生成树的边都会放到A中），我们的目的就是求出A。
算法从S = { u0 } (u0 ∈ V)，A = { }（u0是切完的顶点，比如从顶点u0的outEdges开始切，切完后把顶点u0放到S中）开始，重复执行下述操作，直到S = V为止（数量相等就意味着顶点全部切完了，此时组成最小生成树的边也就有了。此处也可以使用A = V - 1表示，即最小生成树的边数量 = 顶点数量 - 1）。
找到切分C = (S，V – S)的最小横切边(u0，v0)（v0是横切边的另一个顶点）并入集合A，同时将v0并入集合S。

下面就通过图例的方式看一下流程是怎么走的（上面的描述可能有点绕，建议往下面继续看，图例看完后再返回来看上面的描述就明白是什么意思了）：

2.3.1. 执行过程

从顶点A的outEdges开始切；

最小横切边是AB，S = { A, B }, A = { AB }，按照C = (S，V – S)切分；

最小横切边是BC和AH，任选其中一条边（如BC），S = { A, B, C }, A = { AB, BC }，按照C = (S，V – S)继续切分；

最小横切边是CI，S = { A, B, C, I }, A = { AB, BC, CI }，按照C = (S，V – S)继续切分；

最小横切边是CF，S = { A, B, C, I, F }, A = { AB, BC, CI, CF }，按照C = (S，V – S)继续切分；

最小横切边是FG，S = { A, B, C, I, F, G }, A = { AB, BC, CI, CF, FG }，按照C = (S，V – S)继续切分；

最小横切边是HG，S = { A, B, C, I, F, G, H }, A = { AB, BC, CI, CF, FG, GH }，按照C = (S，V – S)继续切分；

最小横切边是CD，S = { A, B, C, I, F, G, H, D }, A = { AB, BC, CI, CF, FG, GH, CD }，按照C = (S，V – S)继续切分；

最小横切边是DE，S = { A, B, C, I, F, G, H, D, E }, A = { AB, BC, CI, CF, FG, GH, CD, DE }，此时发现S的数量和顶点集数量相等，停止切分；

把顶点按照A中的边连接起来就是最小生成树；

Prim算法的核心就是不断切分，每次取横切边权值最小的边，最终连接起来就是一个最小生成树。

2.3.2. 具体实现

Java官方的PriorityQueue底层实现逻辑是最小堆，虽然我们也可以使用它获取顶点出边的最小值，但实现起来比较麻烦（PriorityQueue构造器不满足我们的需求，不能同时传比较器和集合），所以我们可以自己实现最小堆（基本逻辑不变，主要是能够自定义构造方法）。

实现的难点就是如何切分，具体细节请看下面代码（有注释）。并且要防止记录重复边，因为连通图是无向的（如，顶点A和B都有入边和出边，并且是相互指向对方，当需要把顶点B的出边加入到堆中时，也会把B到A的边也加进去）。

// 抽象类（图的公共方法都在这里）
public abstract class Graph<V, E> {
  protected WeightManager<E> weightManager;
  
  public Graph(WeightManager<E> weightManager) {
    this.weightManager = weightManager;
  }

  // 自定义比较器
  public interface WeightManager<E> {
    int compare(E w1, E w2);
  }
  // other code...
}

// 图的实现
public class ListGraph<V, E> extends Graph<V, E> {
  public ListGraph(WeightManager<E> weightManager) {
    super(weightManager);
  }

  // 比较器
  private Comparator<Edge<V, E>> edgeComparator = (Edge<V, E> e1, Edge<V, E> e2) -> {
    return weightManager.compare(e1.weight, e2.weight);
  };

  private Set<Edge<V, E>> prim() {
    Iterator<Vertex<V, E>> it = vertices.values().iterator();
    if (!it.hasNext()) return null;
    // 通过迭代器随机找一个入口顶点
    Vertex<V, E> vertex = it.next();
    // 最小生成树的边集（edgeInfos即描述中提到的集合A）
    Set<Edge<V, E>> edgeInfos = new HashSet<>();
    // 最小生成树的顶点（addedVertices即描述中提到的集合S）
    Set<Vertex<V, E>> addedVertices = new HashSet<>();
    addedVertices.add(vertex);
    // 由于获取的是出边的最小值，所以使用最小堆
    MinHeap<Edge<V, E>> heap = new MinHeap<>(vertex.outEdges, edgeComparator);
    int verticesSize = vertices.size();
    // 当S和V数量相等时，意味着最小生成树已经构成（判断条件必须加上，因为堆不一定为空）
    while (!heap.isEmpty() && addedVertices.size() < verticesSize) {
      // 获取最小边并从堆中移除
      Edge<V, E> edge = heap.remove();
      // 防止重复边加入到edgeInfos（连通图是无向的）
      if (addedVertices.contains(edge.to)) continue;
      // 最小边是构成最小生成树的一部分
      edgeInfos.add(edge.info());
      // 构成最小生成树的顶点
      addedVertices.add(edge.to);
      // 从哪开始切分？在代码层面就是堆中的所有边必然是横切边，所以需要把最小边终点的outEdges添加到堆中，用以构造下一个切分
      heap.addAll(edge.to.outEdges);
    }
    return edgeInfos;
  }

  // other code...
}

// 使用
public class Main {
  static WeightManager<Double> weightManager = new WeightManager<Double>() {
    public int compare(Double w1, Double w2) {
      return w1.compareTo(w2);
    }
  }
  Graph<Object, Double> graph = new ListGraph<>(weightManager);
}

时间复杂度：由于堆中元素是动态添加和移除的，所以不太好分析（还有可能用的不是二叉堆，而是斐波那契堆）。如果以二叉堆为例并且最坏情况考虑，原地建堆O(E) + E * 堆操作O(logE) = O(ElogE)，虽然和Kruskal算法时间复杂度一样，但相比Kruskal算法要稍微好一点（Kruskal算法是一次性把堆建好）。

2.4. Kruskal算法

核心：按照边的权重顺序（从小到大）将边加入生成树中，直到生成树中含有V – 1条边为止（V是顶点数量）。若加入该边会与生成树形成环，则不加入该边（从第3条边开始，可能会与生成树形成环）。

为什么是从第3条边开始可能会形成环？

因为第一条边（权值最小边）肯定是组成最小生成树的一部分，而第二条边（权值次小边）可能出现在第一次切分的横切边中，也可能在第二次切分的横切边中，不管是哪种情况，都会成为第二次切分的横切边，又因为第二条边是权值次小边，所以必然也是组成最小生成树的一部分。构成环至少需要三条边，所以从第三条边开始可能会形成环。

2.4.1. 执行过程

选择权值最小边（HG，权值是1）：

选择剩余边的权值最小边（权值是2的IC或GF，我们选择IC）：

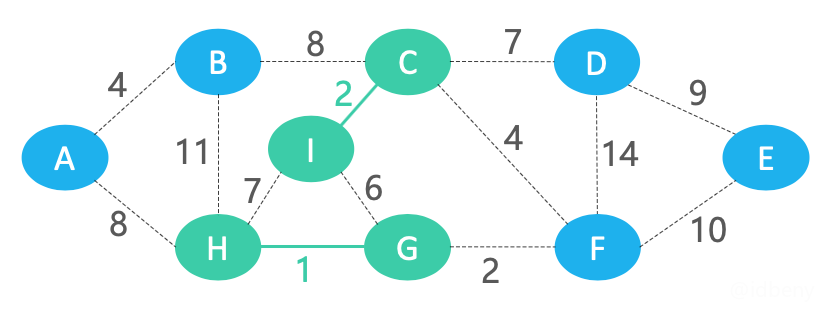
接下来选择边时，就需要判断是否会形成环。

选择剩余边的权值最小边（权值是2的GF）：

选择剩余边的权值最小边（权值是4的AB或CF，我们选择AB）：

选择剩余边的权值最小边（权值是4的CF）：

选择剩余边的权值最小边（权值是6的IG会形成环，因此不能选。继续选择权值是7的CD或HI，由于HI也会形成环，所以不能选。只有CD不会形成环，所以选择权值是7的CD）：

选择剩余边的权值最小边（权值是8的AH或BC，我们选择AH）：

选择剩余边的权值最小边（权值是8的BC会形成环，因此不能选。继续选择权值是9的DE），此时发现选中边的数量等于顶点集数量减1（已经构成最小生成树）：

把选中的边连接起来就是最小生成树：

2.4.2. 具体实现

实现的难点是判断选择的边是否构成环，使用并查集可以做到。所有顶点都加入到并查集让顶点变成一个单集合（初始化），把每次选中边的起点和终点作为合并条件开始合并，如果选中边的起点和终点在同一个集合中（如上面的过程6，I和G就在同一个集合），必然会形成环。

private Set<Edge<V, E>> kruskal() {
  int edgeSize = vertices.size() - 1;
  if (edgeSize == -1) return null;
  // 最小生成树的边集
  Set<Edge<V, E>> edgeInfos = new HashSet<>();
  // 使用最小堆找出权值最小的边
  MinHeap<Edge<V, E>> heap = new MinHeap<>(edges, edgeComparator);
  // 并查集初始化，主要目的是用来判断选中的边是否构成环
  UnionFind<Vertex<V, E>> uf = new UnionFind<>();
  vertices.forEach((V v, Vertex<V, E> vertex) -> {
    uf.makeSet(vertex);
  });
  // 当edgeInfos的数量等于顶点集数量减1时，意味着最小生成树已经构成（判断条件必须加上，因为堆不一定为空）
  while (!heap.isEmpty() && edgeInfos.size() < edgeSize) {
    // 获取最小边并从堆中移除
    Edge<V, E> edge = heap.remove();
    // 判断选择的边是否构成环（起点和终点是否在同一个集合）
    if (uf.isSame(edge.from, edge.to)) continue;
    // 最小边是构成最小生成树的一部分
    edgeInfos.add(edge.info());
    // 合并顶点（让起点和终点到同一个集合）
    uf.union(edge.from, edge.to);
  }
  return edgeInfos;
}

时间复杂度：原地建堆O(E) + 并查集初始化O(V) + E * 堆移除O(logE) = O(ElogE)。