【数据结构与算法】系列三十八 - 动态规划（最长公共子串）

最长公共子串和最长公共子序列的区别就是子串是连续的（同样连续的概念：子数组、子区间），子序列是非连续的。两者的实现思路很像。

一、最长公共子串

最长公共子串（Longest Common Substring），子串是连续的子序列。

题目：求两个字符串的最长公共子串长度。

举例1：ABCBA 和 BABCA 的最长公共子串是ABC，长度为3。

1.1. 思路

假设2个字符串分别是str1、str2，i ∈ [1, str1.length]，j ∈ [1, str2.length]。

1.1.1. 定义状态

假设dp(i, j)是以str1[i – 1]、str2[j – 1]结尾的最长公共子串长度。

比如str1 = "ABCD"，str2 = "BCDAE"：

dp(2, 3)意思是以str1[2 - 1] (B)结尾和str2[3 - 1] (D)结尾的最长公共子串长度，最长公共子串不存在，所以长度是0
dp(4, 3)意思是以str1[4 - 1] (D)结尾和str2[3 - 1] (D)结尾的最长公共子串长度，最长公共子串是BCD，长度是3

1.1.2. 初始状态

dp(i, 0)、dp(0, j)初始值均为0。

1.1.3. 状态转义方程

如果str1[i – 1] == str2[j – 1]，那么dp(i, j) = dp(i – 1, j – 1) + 1
如果str1[i – 1] ≠ str2[j – 1]，那么dp(i, j) = 0

最长公共子串的长度是所有dp(i, j)中的最大值max { dp(i, j) }。

1.2. 实现

private static int lcs(String str1, String str2) {
  if (str1 == null || str2 == null) return 0;
  char[] chars1 = str1.toCharArray();
  if (chars1.length == 0) return 0;
  char[] chars2 = str2.toCharArray();
  if (chars2.length == 0) return 0;
  int[][] dp = new int[chars1.length + 1][chars2.length + 1];
  int max = 0;
  for (int i = 1; i <= chars1.length; i++) {
    for (int j = 1; j <= chars2.length; j++) {
      if (chars1[i - 1] != chars2[j - 1]) continue;
      dp[i][j] = dp[i - 1][j - 1] + 1;
      max = Math.max(dp[i][j], max);
    }
  }
  return max;
}

空间复杂度：$O(n*m)$

时间复杂度：$O(n*m)$

1.2.1. 优化

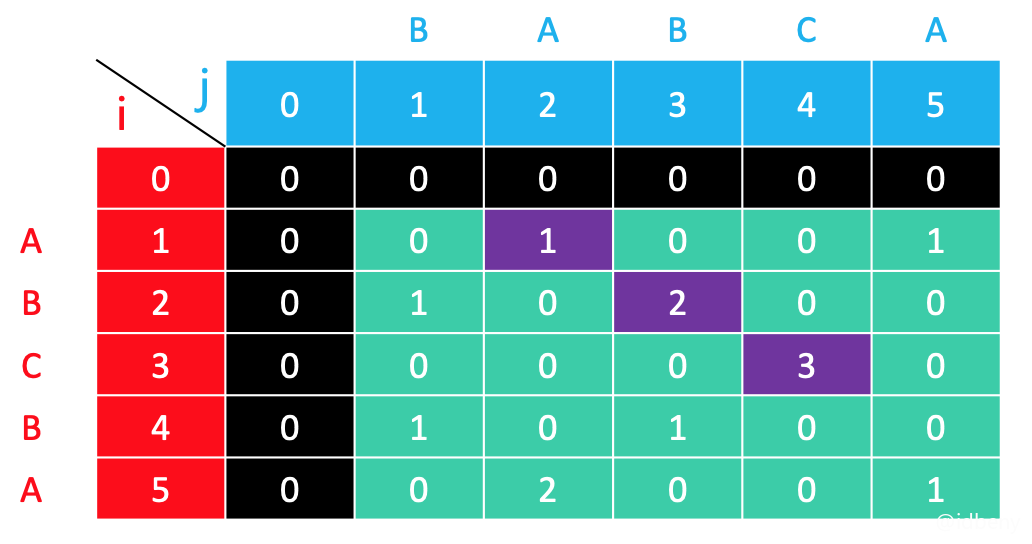
从上图可以看出：

当i和j元素相等时，最长公共子串长度是左上角的值加1，如图中紫色标注部分
如果不相等，就不存在最长公共子串，长度是0。

可以和上一章节的最长公共子序列的优化一样，使用一维数组进行优化（由滚动数组演化而来）。

static int lcs(String str1, String str2) {
  if (str1 == null || str2 == null) return 0;
  char[] chars1 = str1.toCharArray();
  if (chars1.length == 0) return 0;
  char[] chars2 = str2.toCharArray();
  if (chars2.length == 0) return 0;
  char[] rowsChars = chars1, colsChars = chars2;
  if (chars1.length < chars2.length) {
    colsChars = chars1;
    rowsChars = chars2;
  }
  
  int[] dp = new int[colsChars.length + 1];
  int max = 0;
  for (int row = 1; row <= rowsChars.length; row++) {
    int cur = 0;
    for (int col = 1; col <= colsChars.length; col++) {
      int leftTop = cur;
      cur = dp[col];
      if (chars1[row - 1] != chars2[col - 1]) {
        dp[col] = 0;
      } else {
        dp[col] = leftTop + 1;
        max = Math.max(dp[col], max);
      }
    }
  }
  return max;
}

二、0-1背包

0-1背包问题在贪心算法中已经有所描述，但是贪心算法不靠谱，本章节通过动态规划方案对这个问题重新解答。

题目：有n件物品和一个最大承重为W的背包，每件物品的重量是w、价值是v。在保证总重量不超过W的前提下，选择某些物品装入背包，背包的最大总价值是多少？（注意：每个物品只有1件，也就是每个物品只能选择0件或者1件）

2.1. 思路

假设values是价值数组，weights是重量数组。编号为k的物品，价值是values[k]，重量是weights[k]，k ∈ [0, n)。

2.1.1. 定义状态

假设dp(i, j)是最大承重为j、有前i件物品可选时的最大总价值，i ∈ [1, n]，j ∈ [1, W]。

比如values = {6, 3, 5, 4, 6}，weights = {2, 2, 6, 5, 4}：

dp(3, 7)意思是最大承重为7，有前3件物品可选时的最大价值

最终要求的解是dp(n, capacity)，其中capacity是最大承重值（即题目中的W）。

2.1.2. 初始状态

dp(i, 0)、dp(0, j)初始值均为0。

2.1.3. 状态转义方程

如果不选第i个物品（包含超过总重的情况，即j < weights[i – 1]），就需要把第i个物品从可选物品中移除（i - 1），最大承重保持不变（dp(i, j) = dp(i – 1, j)）。
如果选择把第i个物品装入背包，就需要把第装入背包的物品从可选物品中移除（i - 1），同时需要把剩余最大承重减去已选物品的重量（dp(i - 1, j - weights[i - 1])），最终把第i件物品价值加到结果中（dp(i, j) = dp(i - 1, j - weights[i - 1]) + values[i - 1]）。

上面两种情况取最大值即可：dp(i, j) = max { dp(i – 1, j), dp(i – 1, j – weights[i – 1]) + values[i – 1] }

如下图（values = {6, 3, 5, 4, 6}，weights = {2, 2, 6, 5, 4}，capacity = 10）：

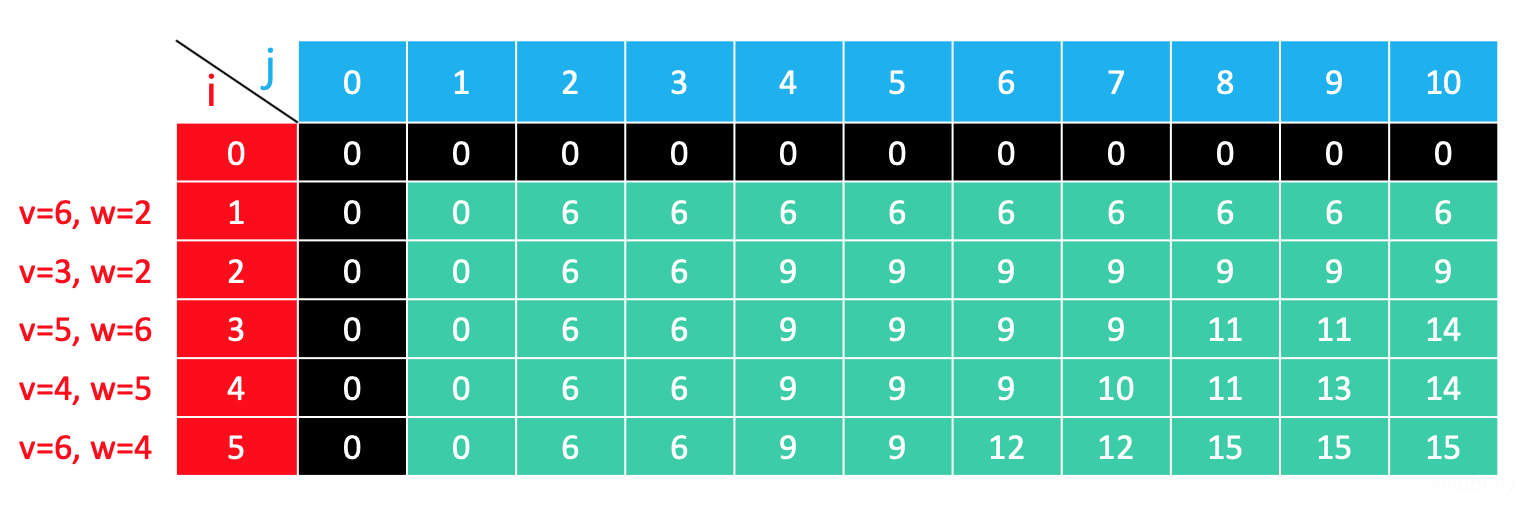
dp(1, 1)：最大承重为1，有前1件物品可选，由于这1件物品的重量（重量：2）超过了最大承重（重量：1），所以这件物品不能放入背包。
- 计算上一件物品（i - 1）是否可以放入背包，由于i - 1 == 0意味着没有物品了，所以dp(1, 1) == 0。
dp(2, 1)：最大承重为2，有前1件物品可选，由于这1件物品的重量（重量：2）未超过最大承重（重量：2），所以这件物品可以放入背包（具有选择权：选或不选）。
- 如果把这件物品放入背包，剩余容量等于0，最大价值就是这件商品的价值（价值：6）；
- 如果这件物品不放入背包，找前面的物品（i - 1）是否可以放入背包，由于i - 1 == 0意味着没有物品了，所以dp(2, 1) == 0；
- 最终取上面两种情况的最大值（价值：6）。
dp(4, 9)：最大承重为9，有前4件物品可选，由于最后一件物品的重量（重量：5）未超过最大承重（重量：9），所以这件物品可以放入背包（具有选择权：选或不选）。
- 如果最后一件物品不放入背包，找前面物品（dp(3, 9)）的最大价值（价值：11）；
- 如果把这件物品放入背包，剩余最大承重是最大承重 - 当前放入背包的物品重量 = 9 - 5 = 4，剩余可选物品是i - 1 = 3件，因此看dp(3, 4)最大价值（价值：9），最终价值是dp(3, 4) + 当前放入背包的物品价值 = 9 + 4 = 13；
- 最终取上面两种情况的最大值（价值：13）。
dp(4, 8)：最大承重为8，有前4件物品可选，由于最后一件物品的重量（重量：5）未超过最大承重（重量：8），所以这件物品可以放入背包（具有选择权：选或不选）。
- 如果最后一件物品不放入背包，找前面物品（dp(3, 8)）的最大价值（价值：11）；
- 如果把这件物品放入背包，剩余最大承重是最大承重 - 当前放入背包的物品重量 = 8 - 5 = 3，剩余可选物品是i - 1 = 3件，因此看dp(3, 3)最大价值（价值：6），最终价值是dp(3, 3) + 当前放入背包的物品价值 = 6 + 4 = 10；
- 最终取上面两种情况的最大值（价值：11）。

总结：

如果j < weights[i – 1]，那么dp(i, j) = dp(i – 1, j)
如果j ≥ weights[i – 1]，那么dp(i, j) = max { dp(i – 1, j), dp(i – 1, j – weights[i – 1]) + values[i – 1] }

2.2. 实现

private static int maxValue(int[] values, int[] weights, int capacity) {
  if (values == null || values.length == 0) return 0;
  if (weights == null || weights.length == 0) return 0;
  if (values.length != weights.length || capacity <= 0) return 0;
  int[][] dp = new int[values.length + 1][capacity + 1];
  for (int i = 1; i <= values.length; i++) {
    for (int j = 1; j <= capacity; j++) {
      if (j < weights[i - 1]) {
        dp[i][j] = dp[i - 1][j];
      } else {
        dp[i][j] = Math.max(
            dp[i - 1][j], 
            values[i - 1] + dp[i - 1][j - weights[i - 1]]);
      }
    }
  }
  return dp[values.length][capacity];
}

2.2.1. 优化

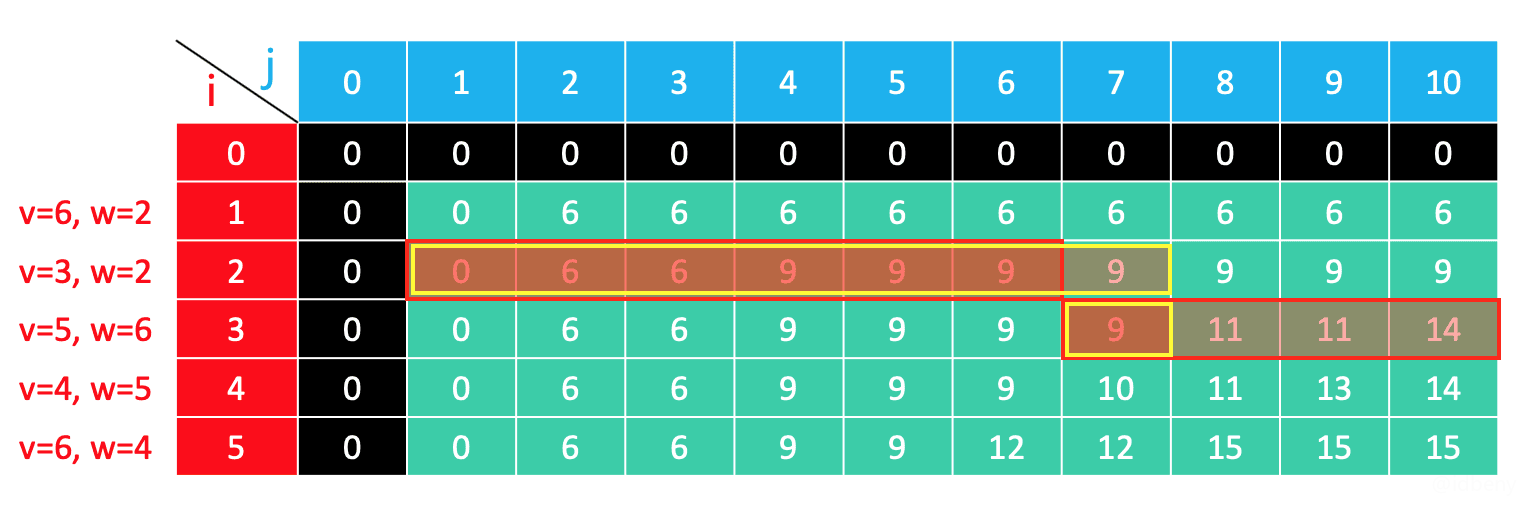
第i行的数据是由它的上一行（第i – 1行）推导出来的，因此可以使用一维数组来优化。但是第j列是不确定的（完全依赖于已选物品的重量），因此我们只能让j的遍历由大到小，否则可能数组中指定位置的值不是我们想要的。

如下图，红色是一维数组范围，黄色是dp(i, j)可能需要用到的数据。

private static int maxValue(int[] values, int[] weights, int capacity) {
  if (values == null || values.length == 0) return 0;
  if (weights == null || weights.length == 0) return 0;
  if (values.length != weights.length || capacity <= 0) return 0;
  int[] dp = new int[capacity + 1];
  for (int i = 1; i <= values.length; i++) {
    /* 优化前
    for (int j = capacity; j >= 1; j--) {
      if (j < weights[i - 1]) continue;
      dp[j] = Math.max(dp[j], values[i - 1] + dp[j - weights[i - 1]]);
    }
    */
    // 优化后
    for (int j = capacity; j >= weights[i - 1]; j--) {
      dp[j] = Math.max(dp[j], values[i - 1] + dp[j - weights[i - 1]]);
    }
  }
  return dp[capacity];
}

2.2.2. 恰好装满

在保证总重量恰好等于最大承重的前提下，选择某些物品装入背包，背包的最大总价值是多少？

dp(i, 0) = 0，总重量恰好为0，最大总价值必然也为0。

dp(0, j) = –∞(负无穷)，j ≥ 1，负数在这里代表无法恰好装满。

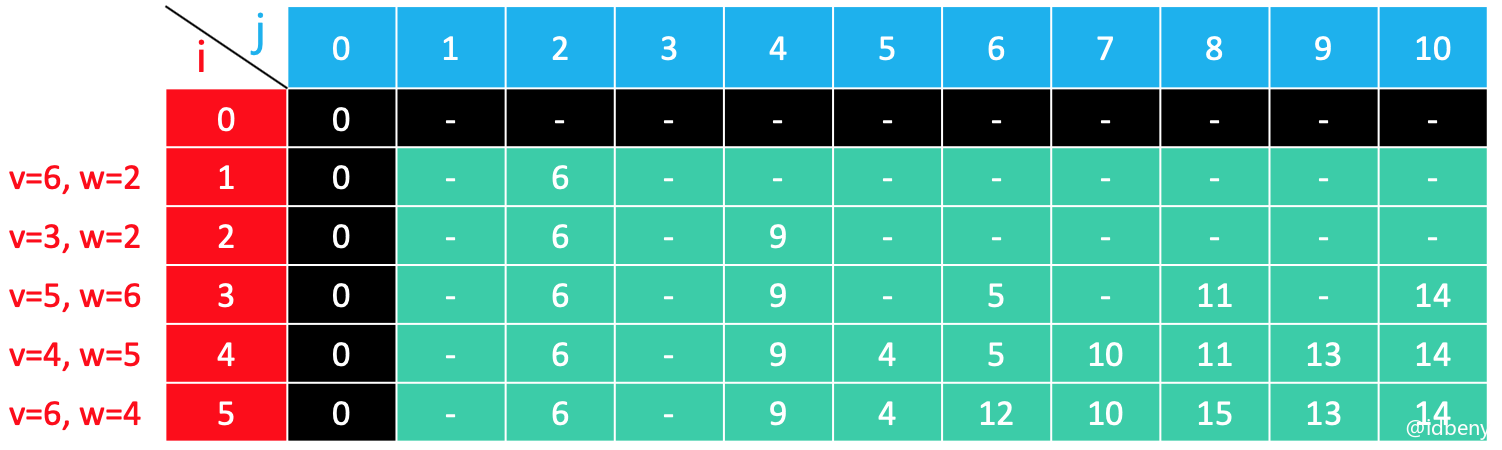
实现和上面的代码基本一致，只需要修改初始值和返回值即可。

/**
 * @return 如果返回-1，代表没法刚好凑到capacity这个容量
 */
static int maxValueExactly(int[] values, int[] weights, int capacity) {
  if (values == null || values.length == 0) return 0;
  if (weights == null || weights.length == 0) return 0;
  if (values.length != weights.length || capacity <= 0) return 0;
  int[] dp = new int[capacity + 1];
  for (int j = 1; j <= capacity; j++) {
    dp[j] = Integer.MIN_VALUE;
  }
  for (int i = 1; i <= values.length; i++) {
    for (int j = capacity; j >= weights[i - 1]; j--) {
      dp[j] = Math.max(dp[j], values[i - 1] + dp[j - weights[i - 1]]);
    }
  }
  return dp[capacity] < 0 ? -1 : dp[capacity];
}