【数据结构与算法】系列三十六 - 动态规划

发表于 | 分类于
| 字数统计 4.4k 字 | 阅读时长 19 分钟

提示：动态规划的概念很难把它描述清楚，所以在看目录一的时候，只需要一眼就过，不需要深入理解。接着往下看目录二的案例，大量的案例会让你理解它的使用套路。当你对几个案例有一定理解后，再回头看目录一的概念性内容就会豁然开朗，然后带着你对概念的理解继续看案例，相信你会兴奋的跳起来。

一、动态规划

动态规划（Dynamic Programming，简称 DP），是求解最优化问题的一种常用策略。

如果经验不足，可能不会立即想到使用动态规划解决问题，只能一步一步优化。怎样才能优化到动态规划呢？

通常的使用套路：

  1. 先使用暴力递归（自顶向下）；
  2. 当出现了重叠子问题时，考虑记忆化搜索（递归的优化版）；
  3. 最后使用递推（自底向上）。

使用套路是针对新手的（不熟悉动态规划），如果你已经对动态规划有深入理解，一般都是使用1.1. 常规步骤。

一般情况下，只要是求最值的问题，都可以使用动态规划解决。

1.1. 常规步骤

动态规划中的“动态”可以理解为是“会变化的状态”。

  1. 定义状态（状态是原问题、子问题的解）
    • 比如定义dp(i)的含义
  2. 设置初始状态（边界）
    • 比如设置dp(0)的值
  3. 确定状态转移方程
    • 比如确定dp(i)和dp(i – 1)的关系

1.2. 相关概念

维基百科：Dynamic Programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions.

  1. 将复杂的原问题拆解成若干个简单的子问题。
  2. 每个子问题仅仅解决1次，并保存它们的解。
  3. 最后推导出原问题的解。

可以用动态规划来解决的问题，通常具备2个特点：

  • 最优子结构（最优化原理）：通过求解子问题的最优解，可以获得原问题的最优解
  • 无后效性
    • 某阶段的状态一旦确定，则此后过程的演变不再受此前各状态及决策的影响（未来与过去无关）
    • 在推导后面阶段的状态时，只关心前面阶段的具体状态值，不关心这个状态是怎么一步步推导出来的

1.2.1. 无后效性

从起点(0, 0)走到终点(4, 4)一共有多少种走法？要求：只能向右、向下走。

假设dp(i, j)是从(0, 0)走到(i, j)的走法：

1
2
3
4
5
// x或y等于0时，只有1个方向，所以只有1中走法
dp(i, 0) = dp(0, j) = 1

// 走到dp(i, j)有两种情况，分别是：dp(i, j – 1)和dp(i – 1, j)
dp(i, j) = dp(i, j – 1) + dp(i – 1, j)

无后效性：推导dp(i, j)时只需要用到dp(i, j – 1)、dp(i – 1, j)的值，不需要关心dp(i, j – 1)、dp(i – 1, j)的值是怎么求出来的。

1.2.2. 有后效性

如果可以向左、向右、向上、向下走，并且同一个格子不能走2次。

有后效性：dp(i, j)下一步要怎么走，还要关心上一步是怎么来的。也就是还要关心dp(i, j – 1)、dp(i – 1, j)是怎么来的。

二、场景示例

2.1. 找零钱

零钱兑换：https://leetcode-cn.com/problems/coin-change/

假设有25分、20分、5分、1分的硬币，现要找给客户41分的零钱，如何办到硬币个数最少？上一章节用贪心策略得到的并非是最优解（贪心得到的解是5枚硬币），如果使用动态规划就能实现最优解（得到的解是3枚硬币）。

假设dp(n)是凑到n分需要的最少硬币个数（这里的假设就是动态规划中的定义状态）：

  • 如果第1次选择了25分的硬币，那么dp(n) = dp(n – 25) + 1。这里的1代表已选择的25分硬币，还剩余n – 25分，下面的选择同理。
  • 如果第1次选择了20分的硬币，那么dp(n) = dp(n – 20) + 1
  • 如果第1次选择了5分的硬币，那么dp(n) = dp(n – 5) + 1
  • 如果第1次选择了1分的硬币，那么dp(n) = dp(n – 1) + 1

第一次选择哪个硬币是不确定的，所以有上面4种可供选择方式。其实本质上就是选择需要最少硬币数的方式，所以dp(n) = min { dp(n – 25), dp(n – 20), dp(n – 5), dp(n – 1) } + 1（最优子问题的解一定可以推出原问题的最优解），这样得到的必然是凑到n分需要的最少硬币个数。

从这也可以看出，动态规划是把所有情况都考虑了，因此可以得到最优解。

2.1.1. 暴力递归

1
2
3
4
5
6
7
8
9
10
int coins(int n) {
  // 防止n是负数
  if (n < 1) return Integer.MAX_VALUE;
  // 递归基
  if (n == 1 || n == 5 || n == 20 || n == 25) return 1;
  // 四种情况取最小值
  int min1 = Math.min(coins(n - 1), coins(n - 5));
  int min2 = Math.min(coins(n - 20), coins(n - 25));
  return Math.min(min1, min2) + 1;
}

类似于斐波那契数列的递归版本，会有大量的重复计算（自顶向下的调用，出现了重叠子问题），时间复杂度较高。

2.1.2. 记忆化搜索

只要包含大量重复计算的情况，就可以在暴利递归的基础上做记忆优化（把重复计算的结果进行存储，当下次遇到同样计算参数时，直接从缓存中查找对应的计算结果，而不必再次计算一遍）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * 记忆化搜索（自顶向下的调用）
 */
static int coins(int n) {
  // 必须输入合法值
  if (n < 1) return -1;
  // db数组存储着凑齐n分需要的最少硬币数（索引：n分，值：最少硬币数）
  // 索引是n，数组长度就需要(n + 1)
  int[] dp = new int[n + 1];
  // 支持的面额数组
  int[] faces = {1, 5, 20, 25};
  for (int face : faces) {
    // faces数组是有序的，所以n < face时，后面的face就没必要设置了
    if (n < face) break;
    // 凑齐face面额硬币需要1枚硬币
    dp[face] = 1;
  }
  return coins(n, dp);
}

static int coins(int n, int[] dp) {
  if (n < 1) return Integer.MAX_VALUE;
  if (dp[n] == 0) {
    // 四种情况取最小值
    int min1 = Math.min(coins(n - 25, dp), coins(n - 20, dp));
    int min2 = Math.min(coins(n - 5, dp), coins(n - 1, dp));
    dp[n] = Math.min(min1, min2) + 1;
  }
  return dp[n];
}

2.1.3. 递推

递推可以认为是非递归。如果是递归，求大的值必须先把小的值求出来。如果我们反过来，先求小的值再求大的值，不仅不需要额外数组辅助，还不需要递归。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * 递推（自底向上）
 */
static int coins(int n) {
  if (n < 1) return -1;
  int[] dp = new int[n + 1];
  for (int i = 1; i <= n; i++) {
    /*
    int min = Integer.MAX_VALUE;
    // 先选择面值为1的硬币
    if (i >= 1) min = Math.min(dp[i - 1], min);
    */

    // 由于i初始值是1，所以上面的两行代码可直接合并为下面一行代码

    // dp[0]默认值是0，当面值为i的硬币是1、5、20、25其中一个时（i硬币被选中），只需要考虑 剩余面值 可供选择的硬币数
    int min = dp[i - 1];
    // 选择面值为5的硬币，看 剩余额度i-5 和 全部使用面值为1的 哪个需要的硬币数更少
    if (i >= 5) min = Math.min(dp[i - 5], min);
    if (i >= 20) min = Math.min(dp[i - 20], min);
    if (i >= 25) min = Math.min(dp[i - 25], min);
    dp[i] = min + 1;
  }
  return dp[n];
}

时间复杂度、空间复杂度：$O(n)$

在上面代码基础上增加一个功能：请输出找零钱的具体方案（具体是用了哪些面值的硬币）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
static int coins(int n) {
  if (n < 1) return -1;
  int[] dp = new int[n + 1];
  // 重点理解：faces[i]是凑够i分时最后那枚硬币的面值
  int[] faces = new int[dp.length];
  for (int i = 1; i <= n; i++) {
    int min = dp[i - 1];
    faces[i] = 1;

    if (i >= 5 && dp[i - 5] < min) {
      min = dp[i - 5];
      faces[i] = 5;
    }
    if (i >= 20 && dp[i - 20] < min) {
      min = dp[i - 20];
      faces[i] = 20;
    }
    if (i >= 25 && dp[i - 25] < min) {
      min = dp[i - 25];
      faces[i] = 25;
    }
    dp[i] = min + 1;
  }
  print(faces, n);
  return dp[n];
}

static void print(int[] faces, int n) {
  System.out.println("faces=" + Arrays.toString(faces));
  System.out.print("[" + n + "] = ");
  while (n > 0) {
    // n - faces[n] 指的是抛开凑够n分的最后那枚的硬币 剩余的面值（即倒数第2枚）
    System.out.print(faces[n] + " ");
    n -= faces[n];
  }
  System.out.println();
}

/*
 coins(6)
 输出：
 faces=[0, 1, 1, 1, 1, 5, 1]
 [6] = 1 5 

 coins(41)
 输出：
 faces=[0, 1, 1, 1, 1, 5, 1, 1, 1, 1, 5, 1, 1, 1, 1, 5, 1, 1, 1, 1, 20, 1, 1, 1, 1, 25, 1, 1, 1, 1, 5, 1, 1, 1, 1, 5, 1, 1, 1, 1, 20, 1]
 [41] = 1 20 20 
 */

2.1.4. 通用实现

上面的代码主要是针对的固定面值硬币，下面的代码则给用户提供了面值数组入口（并且对数组顺序没有要求）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
static int coins(int n, int[] faces) {
  if (n < 1 || faces == null || faces.length == 0) return -1;
  int[] dp = new int[n + 1];
  for (int i = 1; i <= n; i++) {
    int min = Integer.MAX_VALUE;
    for (int face : faces) {
      // 面额不存在
      if (i < face) continue;
      // i - face 代表剩余钱数需要的最少硬币数，如果等于-1，就是没找到
      int v = dp[i - face];
      // v < 0（就是-1） 代表没有面额可供选择  
      // v >= min 指的是这个面额比上次选择的面额所需最少硬币还多
      if (v < 0 || v >= min) continue;
      min = v;
    }
    if (min == Integer.MAX_VALUE) {
      dp[i] = -1;
    } else {
      dp[i] = min + 1;
    }
  }
  return dp[n];
}

2.2. 最大连续子序列和

给定一个长度为n的整数序列，求它的最大连续子序列和。

比如–2、1、–3、4、–1、2、1、–5、4的最大连续子序列和是4 + (–1) + 2 + 1 = 6。

2.2.1. 定义状态

最大连续子序列一定是以某一个数值为结尾的，所以只需要计算以某个数值结尾的子序列和即可。

假设dp(i)是以nums[i]结尾的最大连续子序列和（nums是整个序列）：

  • 以nums[0] (-2)结尾的最大连续子序列是–2，所以dp(0) = –2
  • 以nums[1] (1)结尾的最大连续子序列是1，所以dp(1) = 1
  • 以nums[2] (-3)结尾的最大连续子序列是1、–3，所以dp(2) = dp(1) + (–3) = –2
  • 以nums[3] (4)结尾的最大连续子序列是4，所以dp(3) = 4
  • 以nums[4] (-1)结尾的最大连续子序列是4、–1，所以dp(4) = dp(3) + (–1) = 3
  • 以nums[5] (2)结尾的最大连续子序列是4、–1、2，所以dp(5) = dp(4) + 2 = 5
  • 以nums[6] (1)结尾的最大连续子序列是4、–1、2、1，所以dp(6) = dp(5) + 1 = 6
  • 以nums[7] (-5)结尾的最大连续子序列是4、–1、2、1、–5，所以dp(7) = dp(6) + (–5) = 1
  • 以nums[8] (4)结尾的最大连续子序列是4、–1、2、1、–5、4，所以dp(8) = dp(7) + 4 = 5

2.2.2. 初始状态

dp(0)的值是nums[0]。

2.2.3. 状态转移方程

状态转移方程一定是求dp(i)和dp(i – 1)的关系。如果dp(i)前面的子序列dp(i – 1)和是负数，就没有必要把前面的数加进来，并且它的最大子序列和一定是自己。如果是正数，就把前面的子序列和一并算进来。

总结如下：

  • 如果dp(i – 1) ≤ 0，那么dp(i) = nums[i]
  • 如果dp(i – 1) > 0，那么dp(i) = dp(i – 1) + nums[i]

2.2.4. 具体实现

最大连续子序列和是所有dp(i)中的最大值max { dp(i) }，i ∈ [0, nums.length)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
private int maxSubArray(int[] nums) {
  if (nums == null || nums.length == 0) return 0;
  int[] dp = new int[nums.length];
  dp[0] = nums[0];
  int max = dp[0];
  for (int i = 1; i < dp.length; i++) {
    int prev = dp[i - 1];
    if (prev <= 0) {
      dp[i] = nums[i];
    } else {
      dp[i] = prev + nums[i];
    }
    max = Math.max(dp[i], max);
  }
  return max;
}

空间复杂度：$O(n)$

时间复杂度：$O(n)$

由于我们只需要求最大和，不需要保存其他子序列和，因此可以优化一下内存空间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
private int maxSubArray(int[] nums) {
  if (nums == null || nums.length == 0) return 0;
  int dp = nums[0];
  int max = dp;
  for (int i = 1; i < nums.length; i++) {
    if (dp <= 0) {
      dp = nums[i];
    } else {
      dp = dp + nums[i];
    }
    max = Math.max(dp, max);
  }
  return max;
}

空间复杂度：$O(1)$

时间复杂度：$O(n)$

2.3. 最长上升子序列

最长上升子序列（Longest Increasing Subsequence，简称 LIS)，也叫最长递增子序列。

最长上升子序列：https://leetcode-cn.com/problems/longest-increasing-subsequence/

题目：给定一个无序的整数序列，求出它最长上升子序列的长度（要求严格上升，意思是相等不算）。

比如[10, 2, 2, 5, 1, 7, 101, 18]的最长上升子序列是[2, 5, 7, 101]、[2, 5, 7, 18]，长度是4。

2.3.1. 动态规划

2.3.1.1. 状态定义

假设nums = [10, 2, 2, 5, 1, 7, 101, 18]，dp(i)是以nums[i]结尾的最长上升子序列的长度（i ∈ [0, nums.length)）。

  • 以nums[0] (10)结尾的最长上升子序列是10，所以dp(0) = 1
  • 以nums[1] (2)结尾的最长上升子序列是2，所以dp(1) = 1
  • 以nums[2] (2)结尾的最长上升子序列是2，所以dp(2) = 1
  • 以nums[3] (5)结尾的最长上升子序列是2、5，所以dp(3) = dp(1) + 1 = dp(2) + 1 = 2
  • 以nums[4] (1)结尾的最长上升子序列是1，所以dp(4) = 1
  • 以nums[5] (7)结尾的最长上升子序列是2、5、7，所以dp(5) = dp(3) + 1 = 3
  • 以nums[6] (101)结尾的最长上升子序列是2、5、7、101，所以dp(6) = dp(5) + 1 = 4
  • 以nums[7] (18)结尾的最长上升子序列是2、5、7、18，所以dp(7) = dp(5) + 1 = 4

最长上升子序列的长度是所有dp(i)中的最大值max { dp(i) }，i ∈ [0, nums.length)。

要计算dp(i)的最长上升子序列，需要把i之前的元素都遍历一遍，这样才能找到目标。如果没有找到比i小的元素，最长上升子序列就是当前元素（这里就可以看出，dp(i)默认值是1）。

2.3.1.2. 初始状态

dp(0) = 1，所有的dp(i)默认都初始化为1。

2.3.1.3. 状态转移方程

遍历j ∈ [0, i)：

  • 当nums[i] > nums[j]，nums[i]可以接在nums[j]后面，形成一个比dp(j)更长的上升子序列，长度为dp(j) + 1，最终dp(i) = max { dp(i), dp(j) + 1 }
  • 当nums[i] ≤ nums[j]，nums[i]不能接在nums[j]后面，跳过此次遍历（continue）。
2.3.1.4. 具体实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
static int lengthOfLIS1(int[] nums) {
  if (nums == null || nums.length == 0) return 0;
  int[] dp = new int[nums.length];
  int max = dp[0] = 1;
  for (int i = 1; i < dp.length; i++) {
    dp[i] = 1;
    for (int j = 0; j < i; j++) {
      if (nums[i] <= nums[j]) continue;
      dp[i] = Math.max(dp[i], dp[j] + 1);
    }
    max = Math.max(dp[i], max);
  }
  return max;
}

空间复杂度：$O(n)$

时间复杂度：$O(n^2)$

2.3.2. 二分搜索

2.3.2.1. 思路

  • 把每个数字看做是一张扑克牌，从左到右按顺序处理每一个扑克牌。
  • 如果牌顶 ≥ 选择的扑克牌，将选择的扑克牌压在牌顶对应的牌堆上面。
  • 如果牌顶 < 选择的扑克牌，就在最右边新建一个牌堆，将选择的扑克牌放入这个新牌堆中。
  • 当处理完所有牌，最终牌堆的数量就是最长上升子序列的长度。

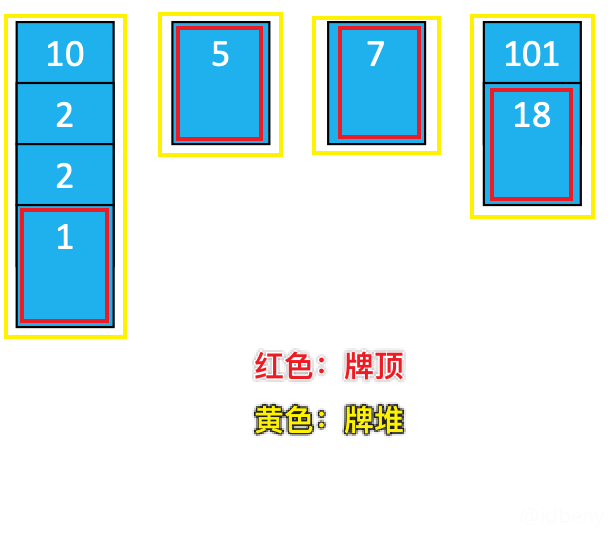
核心：只要拿到的扑克牌比牌顶大（或相等），就重新开始计算最长上升子序列的长度（即牌堆的数量）。

2.3.2.2. 实现

代码不会具体体现牌堆，而是直接在数组的对应位置（虚拟牌堆）进行牌顶覆盖。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
private static int lengthOfLIS(int[] nums) {
  if (nums == null || nums.length == 0) return 0;
  // 牌堆的数量
  int len = 0;
  // 牌顶数组
  int[] top = new int[nums.length];
  // 遍历所有的牌
  for (int num : nums) {
    int j = 0;
    while (j < len) {
      // 找到一个>=num的牌顶
      if (top[j] >= num) {
        top[j] = num;
        break;
      }
      // 牌顶 < num
      j++;
    }
    if (j == len) { // 新建一个牌堆
      len++;
      top[j] = num;
    }
  }
  return len;
}

时间复杂度：$O(n^2)$

空间复杂度：$O(n)$

2.3.2.3. 二分搜索优化

上面的代码时间复杂度是$O(n^2)$，而且牌顶数组是有序的（1, 5, 7, 18），因此当拿到一张牌时，可以使用二分搜索找出牌最终要放入的牌堆位置并覆盖牌顶（有点类似插入排序）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
private static int lengthOfLIS(int[] nums) {
  if (nums == null || nums.length == 0) return 0;
  // 牌堆的数量
  int len = 0;
  // 牌顶数组
  int[] top = new int[nums.length];
  // 遍历所有的牌
  for (int num : nums) {
    int begin = 0;
    int end = len;
    while (begin < end) {
      int mid = (begin + end) >> 1;
      if (num <= top[mid]) {
        end = mid;
      } else {
        begin = mid + 1;
      }
    }
    // 覆盖牌顶
    top[begin] = num;
    // 检查是否要新建一个牌堆
    if (begin == len) len++;
  }
  return len;
}

时间复杂度：$O(nlog{n})$

空间复杂度：$O(n)$