【数据结构与算法】系列三十五 - 贪心/分治

。。。

一、贪心

贪心（Greedy）策略，也称为贪婪策略。每一步都采取当前状态下最优的选择（局部最优解），从而希望推导出全局最优解。

贪心的应用：哈夫曼树，最小生成树算法（Prim、Kruskal），最短路径算法（Dijkstra）。

1.1. 场景示例

1.1.1. 最优装载问题（加勒比海盗）

在北美洲东南部，有一片神秘的海域，是海盗最活跃的加勒比海。有一天，海盗们截获了一艘装满各种各样古董的货船，每一件古董都价值连城，一旦打碎就失去了它的价值。海盗船的载重量为W，每件古董的重量为v，海盗们该如何把尽可能多数量的古董装上海盗船？

贪心策略：每一次都优先选择重量最小的古董。

比如W为30，v分别为3、5、4、10、7、14、2、11。

选择重量为2的古董，剩重量28可用；
选择重量为3的古董，剩重量25可用；
选择重量为4的古董，剩重量21可用；
选择重量为5的古董，剩重量16可用；
选择重量为7的古董，剩重量9可用。

最多能装载5个古董。

// 船的载重
int capacity = 30;
// 古董
int[] weights = {3, 5, 4, 10, 7, 14, 2, 11};
// count：已装载古董件数  weight：已装载古董总重量
int count = 0, weight = 0;
Arrays.sort(weights);

for (int i = 0; i < weights.length && weight < capacity; i++) {
  int newWeight = weight + weights[i];
  // 不能超过船的载重
  if (newWeight <= capacity) {
    // 计重
    weight = newWeight;
    // 计数
    count++;
  }
}

1.1.2. 零钱兑换

假设有25分、10分、5分、1分的硬币，现要找给客户41分的零钱，如何办到硬币个数最少？

贪心策略：每一次都优先选择面值最大的硬币。

选择25分的硬币，剩16分；
选择10分的硬币，剩6分；
选择5分的硬币，剩1分；
选择1分的硬币。

最终的解是共4枚硬币。

Integer[] faces = {25, 10, 5, 1};
Array.sort(faces);
// 硬币个数
int coins = 0;
// 给客户的钱
int money = 41;
// 从最大值开始找
int idx = faces.length - 1;
while (idx >= 0) {
  // 选完最大值的硬币后，可能下一次还需要最大的硬币
  while (money >= faces[idx]) {
    money -= faces[idx];
    // 计数
    coins++;
  }
  // 剩余的钱 < 当前硬币值，这时就需要更小的面值硬币
  idx--;
}

假设有25分、20分、5分、1分的硬币，现要找给客户41分的零钱，如何办到硬币个数最少？

贪心策略：每一步都优先选择面值最大的硬币。

选择25分的硬币，剩16分
选择5分的硬币，剩11分
选择5分的硬币，剩6分
选择5分的硬币，剩1分
选择1分的硬币

最终的解是1枚25分、3枚5分、1枚1分的硬币，共5枚硬币。实际上本题的最优解是2枚20分、1枚1分的硬币，共3枚硬币。为什么会这样呢？这就需要了解一下贪心策略的优缺点了。

1.2. 优缺点

贪心策略并不一定能得到全局最优解，而且不会把所有情况都考虑（暴力求解），贪图眼前局部的利益最大化，看不到长远未来，走一步看一步。

优点：简单、高效、不需要穷举所有可能，通常作为其他算法的辅助算法来使用。

缺点：鼠目寸光，不从整体上考虑其他可能，每次采取局部最优解，不会再回溯，因此很少情况会得到最优解（得不到正确的结果）。

1.3. 场景：0-1背包

有n件物品和一个最大承重为W的背包，每件物品的重量是v、价值是p。在保证总重量不超过W的前提下，将哪几件物品装入背包，可以使得背包的总价值最大？（注意:每个物品只有1件，也就是每个物品只能选择0件或者1件，因此称为0-1背包问题）

如果采取贪心策略，有3个方案：

价值主导：优先选择价值最高的物品放进背包
重量主导：优先选择重量最轻的物品放进背包（装的越多价值可能就越大）
价值密度主导：优先选择价值密度最高的物品放进背包（价值密度 = 价值 ÷ 重量）

上面3个方案都是从不同角度出发实现背包的总价值最大，但哪一个才是正确的呢？貌似3个方案都可以实现价值最大，因此也可以说明贪心策略不靠谱（只考虑当前利益最大化，不考虑长远化）。

假设背包最大承重150，7个物品如表格所示：

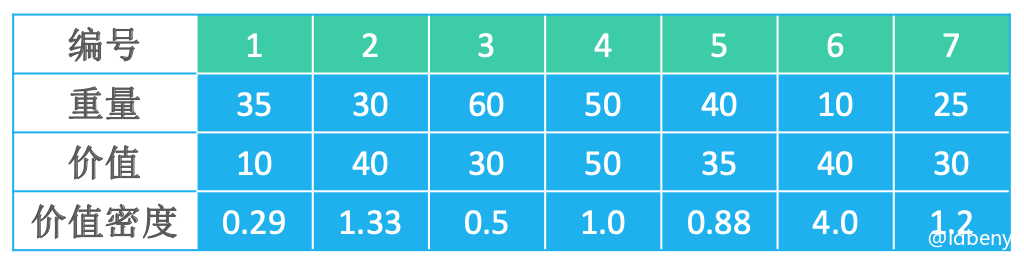
价值主导：放入背包的物品编号是4、2、6、5，总重量130，总价值165。
重量主导：放入背包的物品编号是6、7、2、1、5，总重量140，总价值155。
价值密度主导：放入背包的物品编号是6、2、7、4、1（由于6、2、7、4的总重量是115，还剩下35的容量，所以5和3都不能选），总重量150，总价值170。

从上可以看出，价值密度主导是最优解。

// 物品
public class Article {
  // 重量
  public int weight;
  // 价值
  public int value;
  // 价值密度
  public double valueDensity;
  public Article(int weight, int value) {
    this.weight = weight;
    this.value = value;
    valueDensity = value * 1.0 / weight;
  }
  @Override
  public String toString() {
    return "Article [weight=" + weight + ", value=" + value + ", valueDensity=" + valueDensity + "]";
  }
}

// 0-1背包
public class Knapsack {
  public static void main(String[] args) {
    select("价值主导", (Article a1, Article a2) -> {
      return a2.value - a1.value;
    });
    select("重量主导", (Article a1, Article a2) -> {
      return a1.weight - a2.weight;
    });
    select("价值密度主导", (Article a1, Article a2) -> {
      return Double.compare(a2.valueDensity, a1.valueDensity);
    });
  }

  static void select(String title, Comparator<Article> cmp) {
    // 数据参考上面的图
    Article[] articles = new Article[] {
      new Article(35, 10), new Article(30, 40),
      new Article(60, 30), new Article(50, 50),
      new Article(40, 35), new Article(10, 40),
      new Article(25, 30)
    };
    // 让物品按照cmp的顺序排列，使得能够直接使用for循环
    Arrays.sort(articles, cmp);
    // capacity:背包容量  weight:已装入背包的物品总重量  value:已装入背包的物品总价值
    int capacity = 150, weight = 0, value = 0;
    // 放入背包的物品
    List<Article> selectedArticles = new LinkedList<>();
    for (int i = 0; i < articles.length && weight < capacity; i++) {
      int newWeight = weight + articles[i].weight;
      // 总重不能超过背包容量
      if (newWeight <= capacity) {
        // 累加重量
        weight = newWeight;
        // 累加价值
        value += articles[i].value;
        // 放入背包
        selectedArticles.add(articles[i]);
      }
    }
    
    System.out.println("【" + title + "】");
    System.out.println("总价值：" + value);
    for (int i = 0; i < selectedArticles.size(); i++) {
      System.out.println(selectedArticles.get(i));
    }
    System.out.println("-----------------------------");
  }
}

1.4. LeetCode

分发饼干：https://leetcode-cn.com/problems/assign-cookies/
用最少数量的箭引爆气球：https://leetcode-cn.com/problems/minimum-number-of-arrows-to-burst-balloons/
买卖股票的最佳时机 II：https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/
种花问题：https://leetcode-cn.com/problems/can-place-flowers/
分发糖果：https://leetcode-cn.com/problems/candy/

二、分治

分治（Divide And Conquer），也就是分而治之。

它的一般步骤是：

将原问题分解成若干个规模较小的子问题（子问题和原问题的结构一样，只是规模不一样）
子问题又不断分解成规模更小的子问题，直到不能再分解（直到可以轻易计算出子问题的解）
利用子问题的解推导出原问题的解。

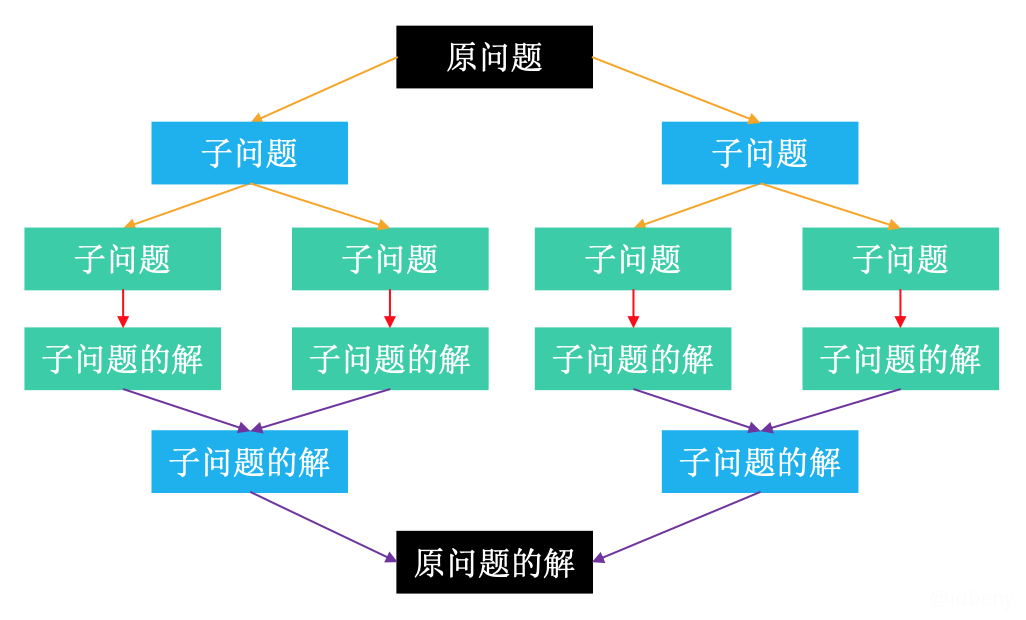
因此，分治策略非常适合用递归。需要注意的是子问题之间是相互独立的。

分治的应用：快速排序，归并排序，Karatsuba算法（大数乘法）。

2.1. 主定理

分治策略通常遵守一种通用模式，解决规模为$n$的问题，分解成$a$个规模为$\frac{n}{b}$的子问题，然后在$O(n^d)$时间内将子问题的解合并起来.

算法运行时间：

$T(n) = aT(\frac{a}{b}) + O(n^d)，a > 0, : b > 1, : d\geqslant0$

$d > \log_b{a} :, \quad T(n) = O(n^d)$

$d = \log_b{a} :, \quad T(n) = O(n^d{\log{n}})$

$d < \log_b{a} :, \quad T(n) = O(n^{\log_b{a}})$

比如归并排序的运行时间是：$T(n) = 2T(\frac{n}{2}) + O(n), : a = 2, b = 2, d = 1$，所以$: T(n) = O(n\log{n})$。

思考：为什么有些问题采取分治策略后，性能会有所提升？

比如要对n个数据进行排序，时间复杂度是$O(n^2)$。如果数据分成两半分别进行排序，即$\frac{n}{2}$、$\frac{n}{2}$，时间复杂度是$O(\frac{n^2}{4})$、$O(\frac{n^2}{4})$。假设子数据合并时的时间复杂度是$O(merge)$，总的时间复杂度就是$O(\frac{n^2}{4}) + O(\frac{n^2}{4}) + O(merge) = O(\frac{n^2}{2}) + O(merge)$。如果$O(merge) < O(\frac{n^2}{2})$，采用分治策略的效率肯定是比之前要高的，一般情况下，合并操作的时间复杂度是$O(n)$，所以采取分治策略后性能会有所提升。

2.2. 最大连续子序列和

最大子序和：https://leetcode-cn.com/problems/maximum-subarray/

题目：给定一个长度为n的整数序列，求它的最大连续子序列和。

比如–2、1、–3、4、–1、2、1、–5、4的最大连续子序列和是4 + (–1) + 2 + 1 = 6。

这道题也属于最大切片问题（最大区段，Greatest Slice）

概念区分：子序列就是从给定的序列中随机挑选出一部分组成一个新的序列（可能连续，也可能不连续）。连续子序列就是子序列中的数据在原序列中必须是连续的。子串、子数组、子区间都是必须连续的数据。

2.2.1. 解法1：暴力出奇迹

穷举出所有可能的连续子序列，并计算出它们的和，最后取它们中的最大值。

public static void main(String[] args) {
  int[] nums = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
  System.out.println(maxSubArray(nums));
}
static int maxSubarray(int[] nums) {
  if (nums == null || nums.length == 0) return 0;
  int max = Integer.MIN_VALUE;
  for (int begin = 0; begin < nums.length; begin++) {
    for (int end = begin; end < nums.length; end++) {
      int sum = 0;
      /* 第1种方式，时间复杂度：O(n^3)
      // sum是[begin, end]的和
      for (int i = begin; i <= end; i++) {
        sum += nums[i];
      }
      */
      // 第2种方式，时间复杂度：O(n^2)
      sum += nums[end];
      // 和之前记录的最大值做比较
      max = Math.max(max, sum);
    }
  }
  return max;
}

空间复杂度：$O(1)$

2.2.2. 解法2：分治

将序列均匀地分割成2个子序列，[begin, end) = [begin, mid) + [mid, end)，mid = (begin + end) >> 1。

假设[begin , end)的最大连续子序列和是S[i, j)，那么它有3种可能：

[i, j)存在于[begin, mid)中，同时S[i, j)也是[begin , mid)的最大连续子序列和。
[i, j)存在于[mid, end)中，同时S[i, j)也是[mid , end)的最大连续子序列和。
[i, j)一部分存在于[begin, mid)中，另一部分存在于[mid, end)中。

[i, j) = [i, mid) + [mid, j)

S[i, mid) = max { S[k, mid) }，begin ≤ k < mid

S[mid, j) = max { S[mid, k) }，mid < k ≤ end

public static void main(String[] args) {
  int[] nums = {-2, 1, -3, 4, -1, 2, 1, -5, 4};
  System.out.println(maxSubArray(nums));
}

static int maxSubArray(int[] nums) {
  if (nums == null || nums.length == 0) return 0;
  return maxSubArray(nums, 0, nums.length);
}

/**
 * 求解[begin, end)中最大连续子序列的和
 */
static int maxSubArray(int[] nums, int begin, int end) {
  // 只有1个元素是就是最大值
  if (end - begin < 2) return nums[begin];
  // 分2半
  int mid = (begin + end) >> 1;
  // 找mid左边最大值
  int leftMax = nums[mid - 1];
  int leftSum = leftMax;
  for (int i = mid - 2; i >= begin; i--) {
    leftSum += nums[i];
    leftMax = Math.max(leftMax, leftSum);
  }
  // 找mid右边边最大值
  int rightMax = nums[mid];
  int rightSum = rightMax;
  for (int i = mid + 1; i < end; i++) {
    rightSum += nums[i];
    rightMax = Math.max(rightMax, rightSum);
  }
  // 最大和在中间（左边 + 右边）、最大和在左边、最大和在右边，三个取最大值
  return Math.max(
    leftMax + rightMax, 
    Math.max(
      maxSubArray(nums, begin, mid), 
      maxSubArray(nums, mid, end)
    )
  );
}

空间复杂度：$O(\log{n})$

时间复杂度：$O(n\log{n})$

跟归并排序、快速排序一样，$T(n) = 2T(\frac{n}{2}) + O(n)$。

最大连续子序列和在实际生活应用场景中有很多，比如一个商铺需要计算一年中连续季度最大盈利值是多少，还可以有其他附属需求，比如连续季度是哪几个季度（上面代码中没有记录子串的值，但实现起来非常简单，只需要一个容器记录即可）。

2.3. 大数乘法

2个超大的数（比如2个100位的数），如何进行乘法？

1
2
3

int a = 12334543545254354543;
int b = 65436564535324231234;
int c = a * b;

上面的代码肯定会报错，因为数值已经超过int类型的表示范围，即使把类型换成long long依然会内存溢出。一般这种超大数都会使用字符串进行存储，然后按照小学时学习的乘法运算，在进行n位数之间的相乘时，需要大约进行$n^2$次个位数的相乘。

比如计算36 x 54：

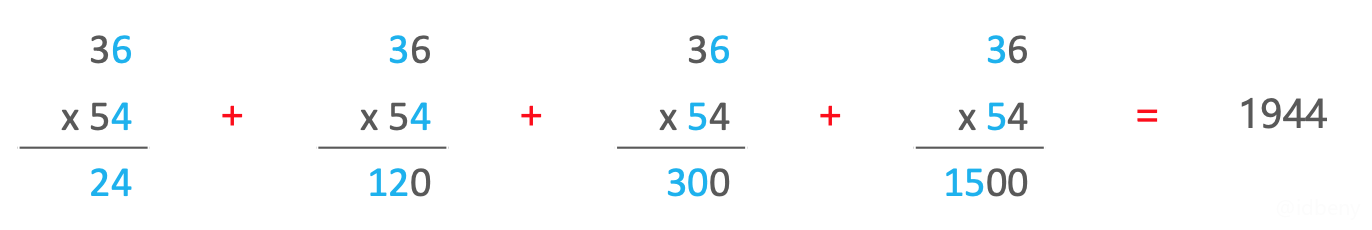
最后的结果1944是24 + 120 + 300 + 1500么？虽然结果是正确的，但不是这样求解的。因为当数值比较大时，高位数的结果可能会出现内存溢出问题。所以正确的处理方法是把每个结果的列数（同位的数值）相加。

  36 
X 54
------
  24
 120 
 300
1500 
------
个位：4
十位：4
百位：9
千位：1

时间复杂度：$T(n) = 4T(\frac{n}{2}) + O(n) = O(n^2)$

1960年Anatolii Alexeevitch Karatsuba提出了Karatsuba算法，提高了大数乘法的效率。

$BC+AD=AC+BD −(A−B)(C−D)$

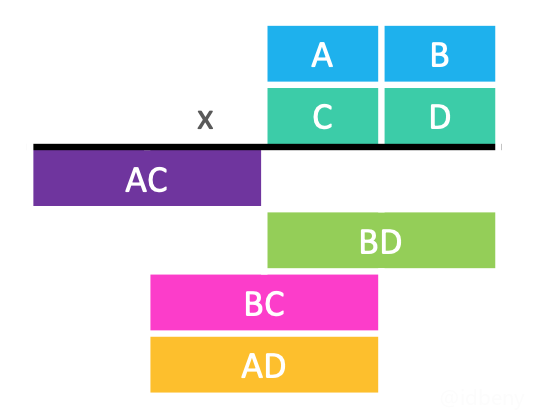
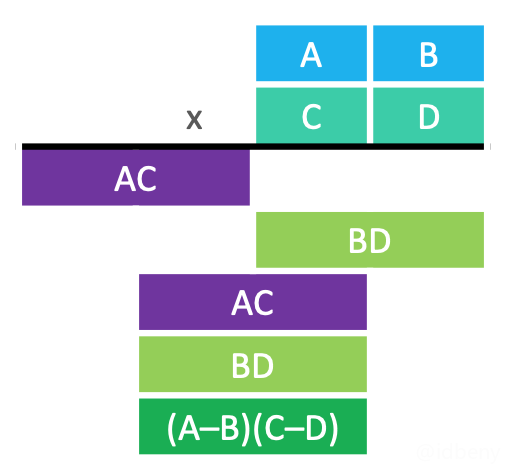
时间复杂度：$T(n) = 3T(\frac{n}{2}) + O(n) = O(n^{1.585})$